1 目的
本文手把手教你在 Mathematica 科学计算软件中搭建机器人的仿真环境,具体包括以下内容:
1 导入机械臂的三维模型
2 正\逆运动学仿真
3 碰撞检测
4 轨迹规划
5 正\逆动力学仿真
6 运动控制
文中的所有代码和模型文件都在此处:https://github.com/robinvista/Mathematica 。使用的软件版本是 Mathematica 11.1,较早的版本可能缺少某些函数,所以最好使用最新版。进入正文之前不妨先看几个例子:




无论你从事的是机器人研发还是教学科研,一款好用的仿真软件都能对你的工作起到很大的帮助。那么应该选择哪个软件呢?最方便的选择就是成熟的商业软件,例如Adams、Webots。你的钱不是白花的,商业软件功能强大又稳定,而且性能一般都经过了优化。可是再强大的商业软件也有设计不合理的地方,它们的算法基本都是“黑箱”,你想做一点更改都不行。从学习和研究的角度出发,最好选择代码可修改的开源或半开源软件。
在论文数据库中检索一下就会发现,很多人都选择借助Matlab这个数学软件平台进行机器人的建模仿真[1]。这并不奇怪,因为Matlab具有优秀的数值计算和仿真能力,在它的基础上开发会很便利。如果你非要舍近求远,用 C++ 编写一套仿真软件,先不要说仿真结果如何显示,光是矩阵计算的实现细节就能让你焦头烂额。
与大名鼎鼎的Matlab 相比,Mathematica在国内知名度并不高,但是不要小看它哦,一旦熟悉了你会刮目相看。我简单对比了一下二者在机器人仿真方面的特点,见下表。由于Mathematica不俗的表现,我选择在它的基础上搭建仿真环境。如果你对Mathematica不熟悉,可以看网络教程,也可以参考我的学习笔记。Mathematica有着陡峭的学习曲线,入门并不容易,其实初学者最快的入门方法就是照着大量的例子演练。本文面向Mathematica的初学者,所以不会使用过于高超的编程技巧。最近,Matlab是推出了机器人仿真工具包和算法库:Robotics System Toolbox,但是价格要一万多元。
| Matlab | Mathematica | ||
| 可视化效果 | 一般 | 优秀 | |
| 导入机器人模型 | 需要自己写函数[1] | 自带函数 | |
| 机器人工具箱/包 | Robotics System Toolbox、Robotic Toolbox[2]、SpaceLib、等 | Screws[3]、Robotica[4]、ModernRobotics等 | |
| 调试功能 | 方便易用 | 目前还不太方便,有点繁琐 | |
| 代码长度(个人经验) | 100 | 20~50 |
1. 获取机器人的外观模型
制作逼真的仿真首先需要的是机器人的外观模型。如果你有机器人的三维模型最好,没有的话也不要紧,著名的机器人制造商都在官网提供其各种型号机器人的真实模型,例如 ABB、安川,供大家免费下载和使用。为了防止山寨,这些模型都是不可通过建模软件直接修改的格式,例如 IGES 和 STEP 格式。但我们只用来显示和碰撞检测,所以并不影响仿真。
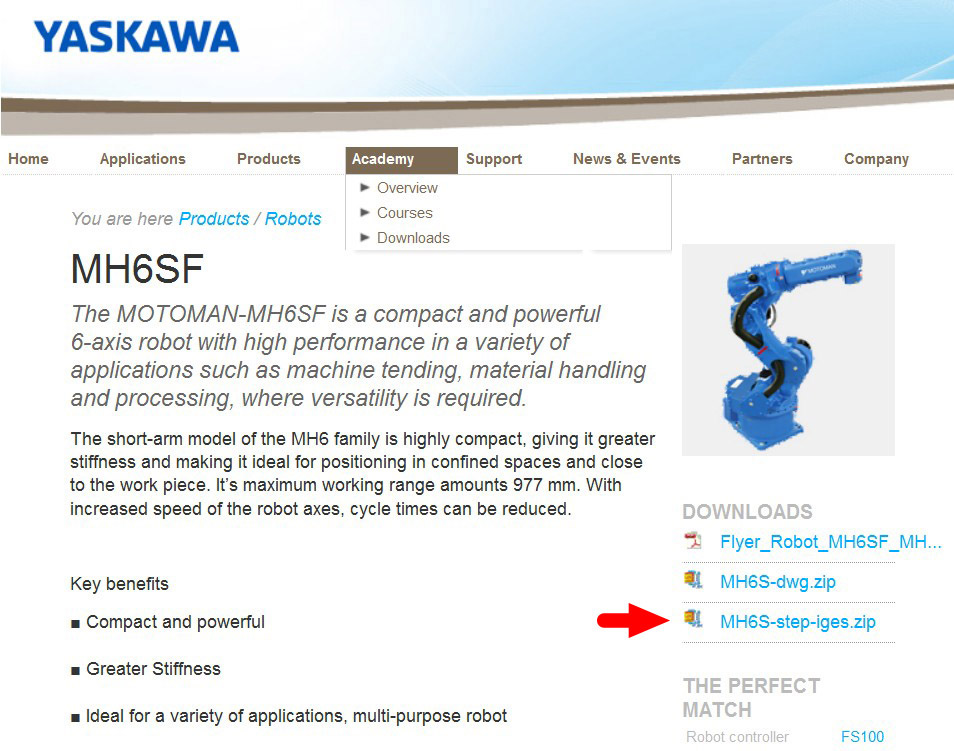
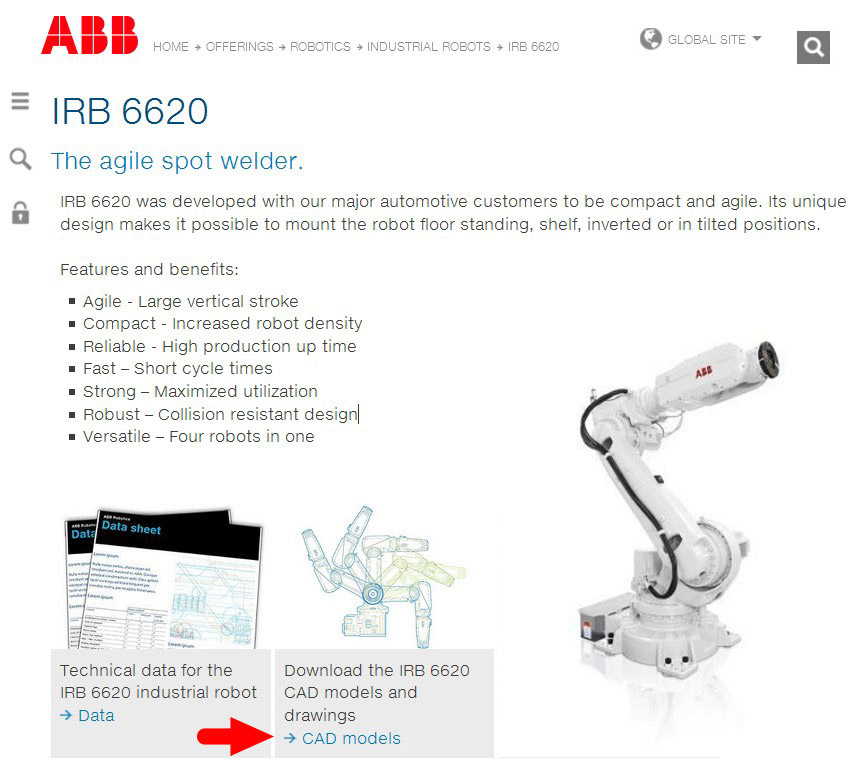
2. 导入机器人的外观模型
获得模型后要导入Mathematica中进行处理并显示,下面我们借助一个例子说明具体的步骤。Motoman ES165D 是安川公司生产的一款6自由度点焊机器人,其最后三个关节轴线相交于一点,这是一种非常经典而且有代表性的设计,因此我们选择以这款机器人为例进行讲解(这个机器人的完整模型点击此处下载)。

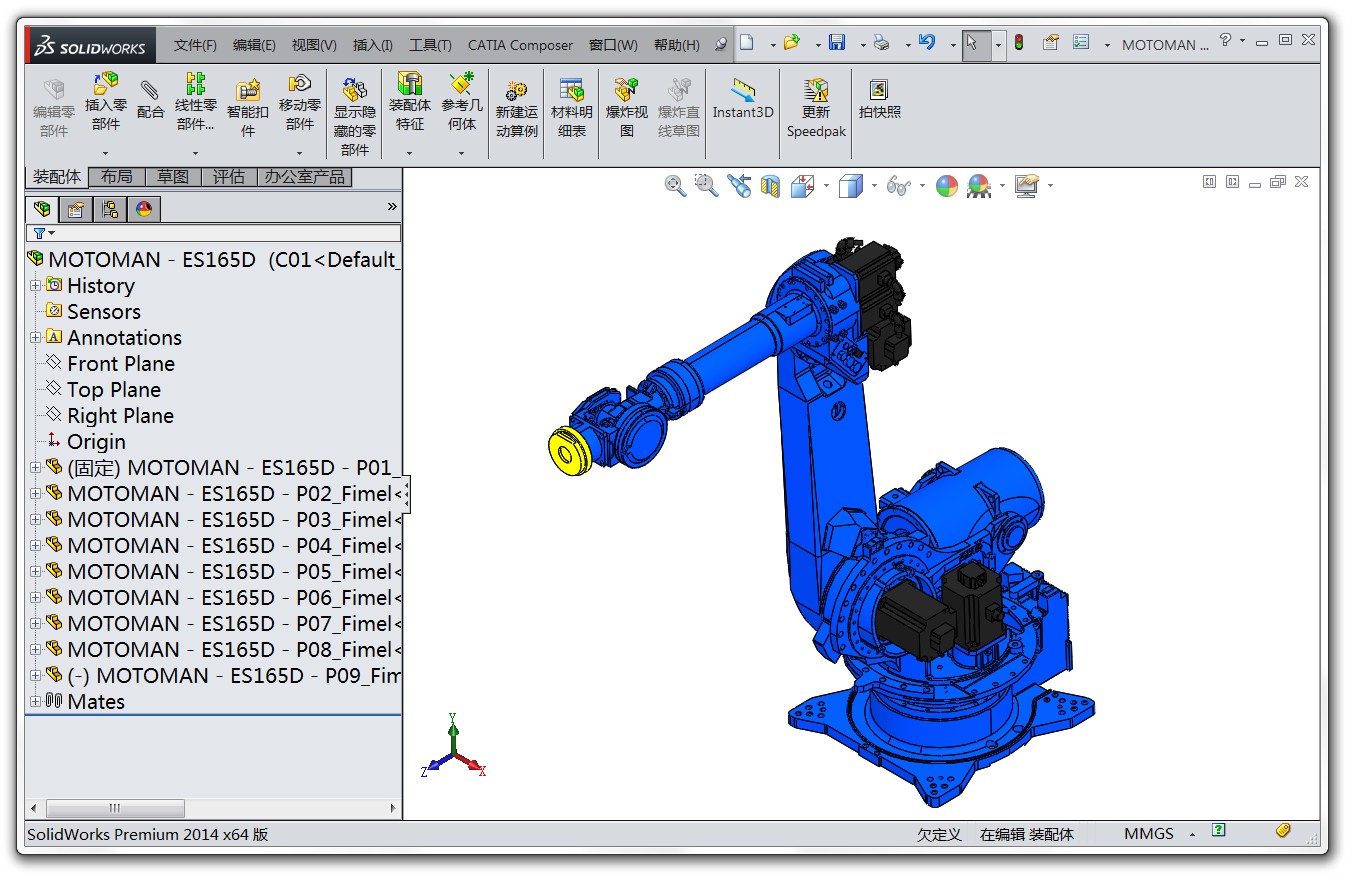
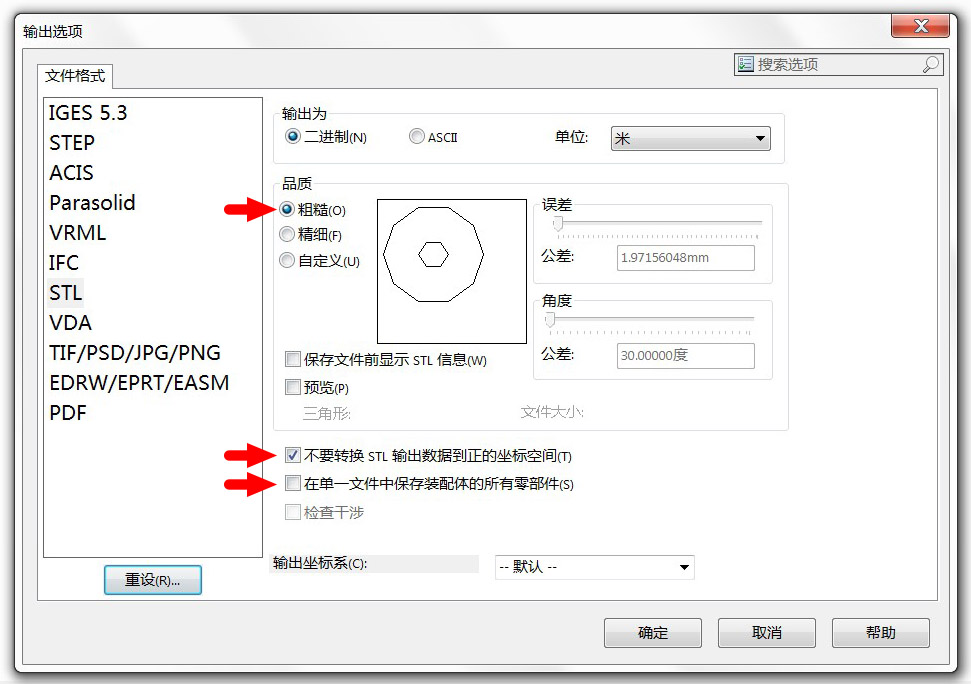
用SolidWorks 2014软件打开机器人的装配体文件,并选择“另存为”STL 格式。然后打开当前页面下方的“选项”对话框,如下图。这里我们要设置三个地方:
1. “品质”表示对模型的简化程度,如果你想实现非常逼真的效果,可以选择“精细”,但缺点是数据点很多导致文件很大、处理起来比较慢。一般选择“粗糙”就够了;
2. 勾选“不要转换 STL 输出数据到正的坐标空间”;
3. 不要勾选“在单一文件中保存装配体的所有连杆”。
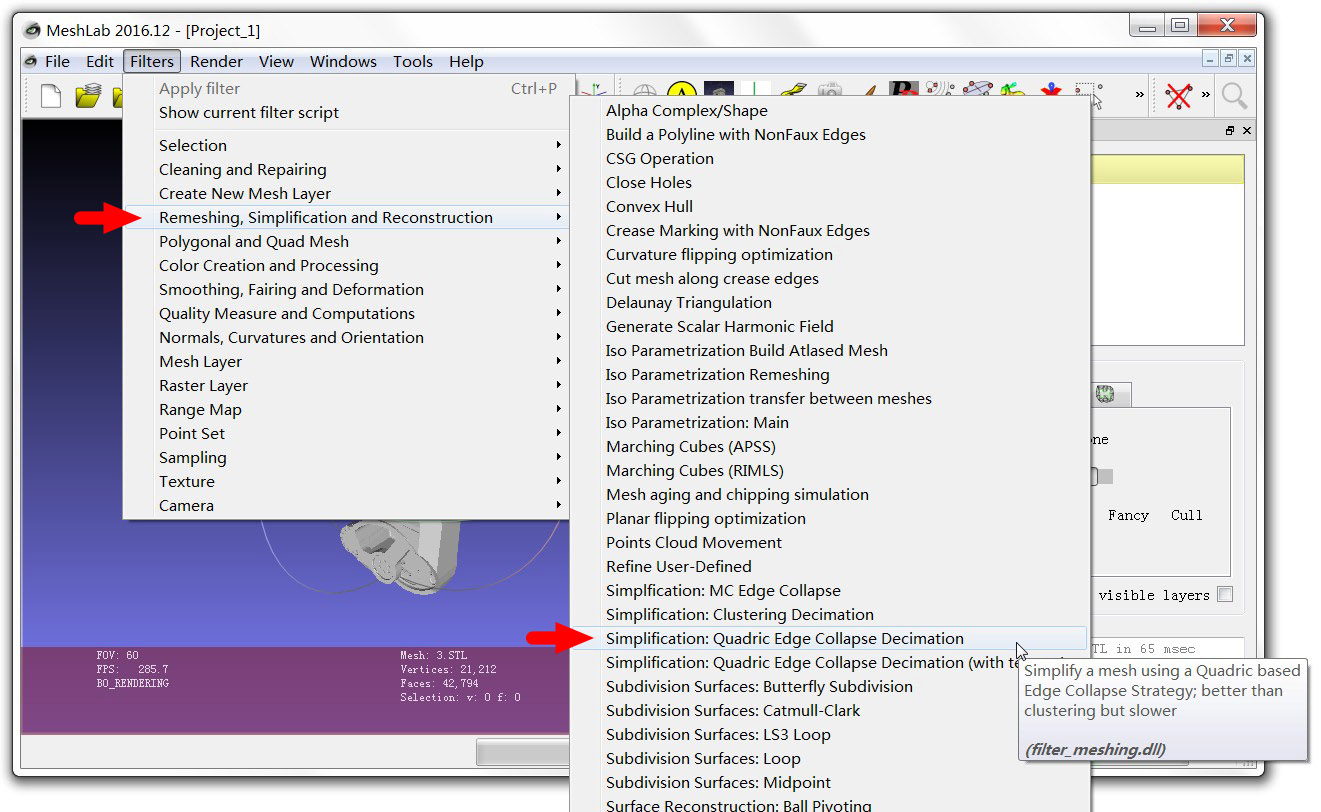
小技巧 STL格式是一种三维图形格式,被很多三维建模软件支持(Mathematica也支持,所以我们要保存为这个格式)。STL格式只存储三维图形的表面信息,而且是用很多的三角形对图形进行近似的表示。如果你的机器人外形比较简单(规则的几何体),那么得到的STL文件大小一般只有几十KB ;可是如果外形很复杂(比如包含很多的孔洞、曲面),生成的STL文件会很大(几MB∼几十MB)。对于一般配置的计算机,模型文件超过100KB用Mathematica处理起来就比较慢了。为了让仿真显示地更流畅,可以利用免费软件MeshLab对其进行化简,MeshLab通常能够在基本不改变外形的前提下将文件大小缩减为原来的十分之一甚至更多。
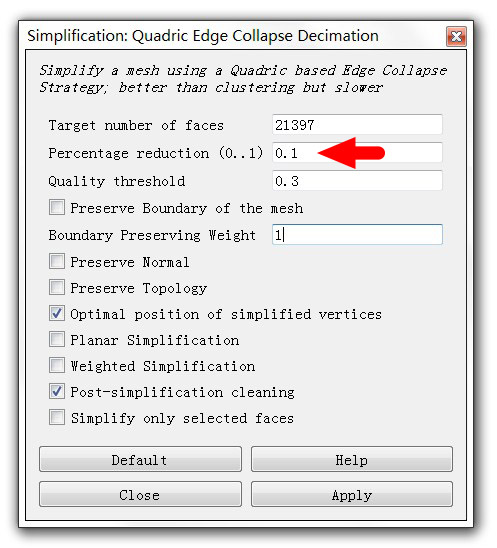
MeshLab的安装和操作都是傻瓜式的,打开后进入如下图左所示的菜单中,出现右图的页面,这里的“Percentage reduction”表示缩减的百分比(1 表示不缩减,0.1 则表示缩减为原来的10%),设置好后点击Apply并保存即可。
然后在 Mathematica中导入 STL 文件,使用的代码如下(假设这些 STL 文件保存在 D:\MOTOMAN 文件夹下):
SetDirectory["D:\\MOTOMAN"]; (*设置文件存放的地址,注意次级路径用双斜杠*)
n = 6; (*n是机械臂的自由度,文章后面还会用到*)
partsName = {"1.stl", "2.stl", "3.stl", "4.stl", "5.stl", "6.stl", "7.stl", "8.stl", "9.stl"}; (*分别是组成机械臂的9个连杆*)
robotPartsGraphics = Import[#, "Graphics3D"] & /@ partsName; (*一次性导入所有连杆,并且导入为可以直接显示的图形格式*)
robotParts = robotPartsGraphics[[;; , 1]]; (*从三维图形中提取出几何数据:顶点的三维坐标和边*)这里我偷了个懒,为了少打些字,我把导出连杆的文件名改成了从1到9的数字(这个机械臂的装配体一共包含9个零件)。我们把导入的模型显示出来,效果如下图。使用的代码如下
Graphics3D[{frame3D, robotParts}]说明
frame3D是三维坐标系的三个正交的轴(xyz轴的颜色分别是RGB)。在机器人领域会用到大量的坐标系及其变换,直接看数字总是不直观,不如将坐标系显示出来更方便。定义frame3D的代码如下,这个坐标系默认原点的位置在(0,0,0),以后我们称这个坐标系为“全局坐标系”。
frame3D = {RGBColor[#], Arrowheads[0.05], Arrow[Tube[{{0, 0, 0}, #}, 0.01]]} & /@ IdentityMatrix[3];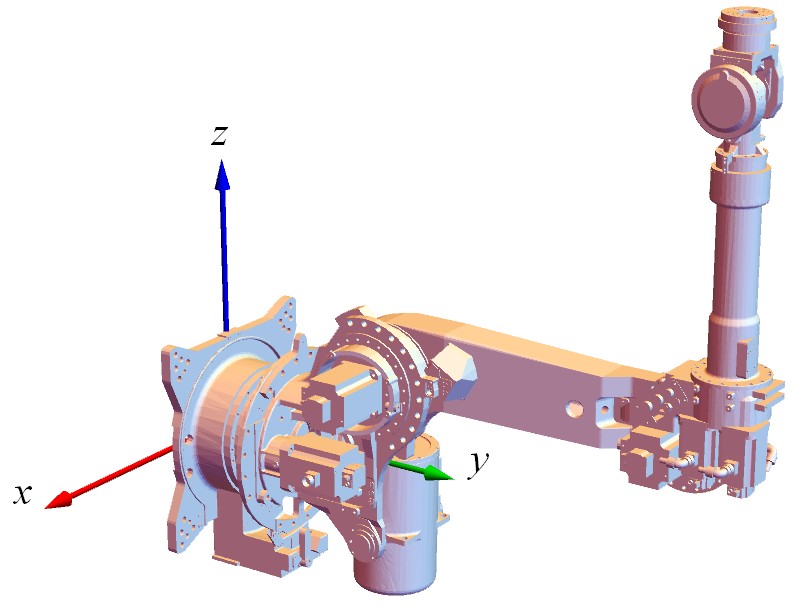

你可能会好奇:导入的零件数据是以什么样的格式储存的呢?
用来存储机器人外形数据的robotParts变量包含一共9个零件的数据,假如你想看第一个零件(对应的是基座,它通常用来将机械臂固定在大地上),可以输入:
robotParts[[1]] (*双层方括号中的数字表示对应第几个零件*) 运行后的输出结果是一堆由 GraphicsComplex 函数包裹着的数字,主要可分为两部分:第一部分是零件几何体所有顶点的三维坐标;第二部分是组成零件几何体的三角形(注意:构成每个三角形的三个顶点是第一部分点的序号,而不是坐标值)。我们可以用以下代码将其分别显示出来:
pts = robotParts[[1]][[1]]; (*零件1的第一部分:顶点的三维坐标数据*)
triangles = robotParts[[1]][[2]]; (*零件1的第二部分:三角形面片*)
trianglesBlue = triangles /. {EdgeForm[] -> EdgeForm[Blue]}; (*三角形的边显示为蓝色*)
Graphics3D[{GraphicsComplex[pts, trianglesBlue], Red, Point[pts]}]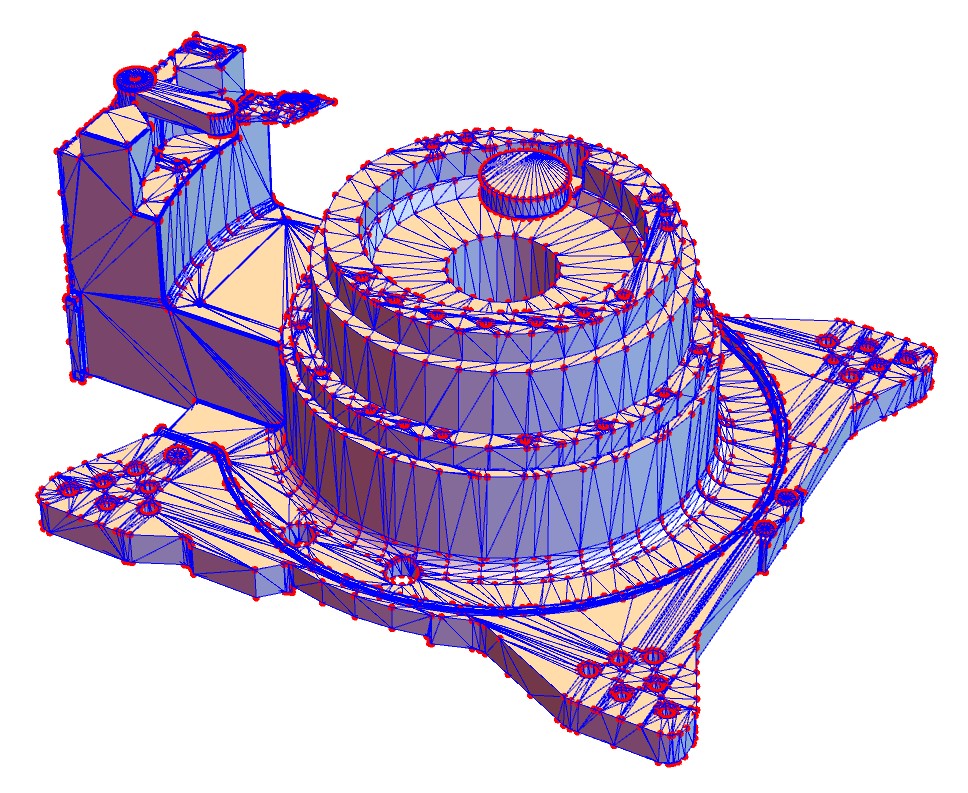
所有零件都成功地导入了,而且它们的相对位置也是正确的。你可能会问:机械臂为什么是处于“躺着”的姿势呢?这是由于零件是按照 SolidWorks 默认的坐标系(y轴向上)绘制和装配的。而在 Mathematica 中默认的坐标系是z轴向上。那么我们采用哪个坐标系呢?
当然你可以任性而为,用哪个都可以。不过根据国家标准GBT 16977-2005 《工业机器人 坐标系和运动命名原则》,机械臂基座坐标系的z轴应该垂直于基座安装面(一般是水平地面)、指向为重力加速度的反方向(也就是垂直地面向上),x轴指向机器人工作空间中心点的方向。制定国家标准的都是些经验丰富的专家老手,我们最好跟国标保持一致(国标的作图水平就不能提高点吗?这图怎么感觉像小学生画的)。

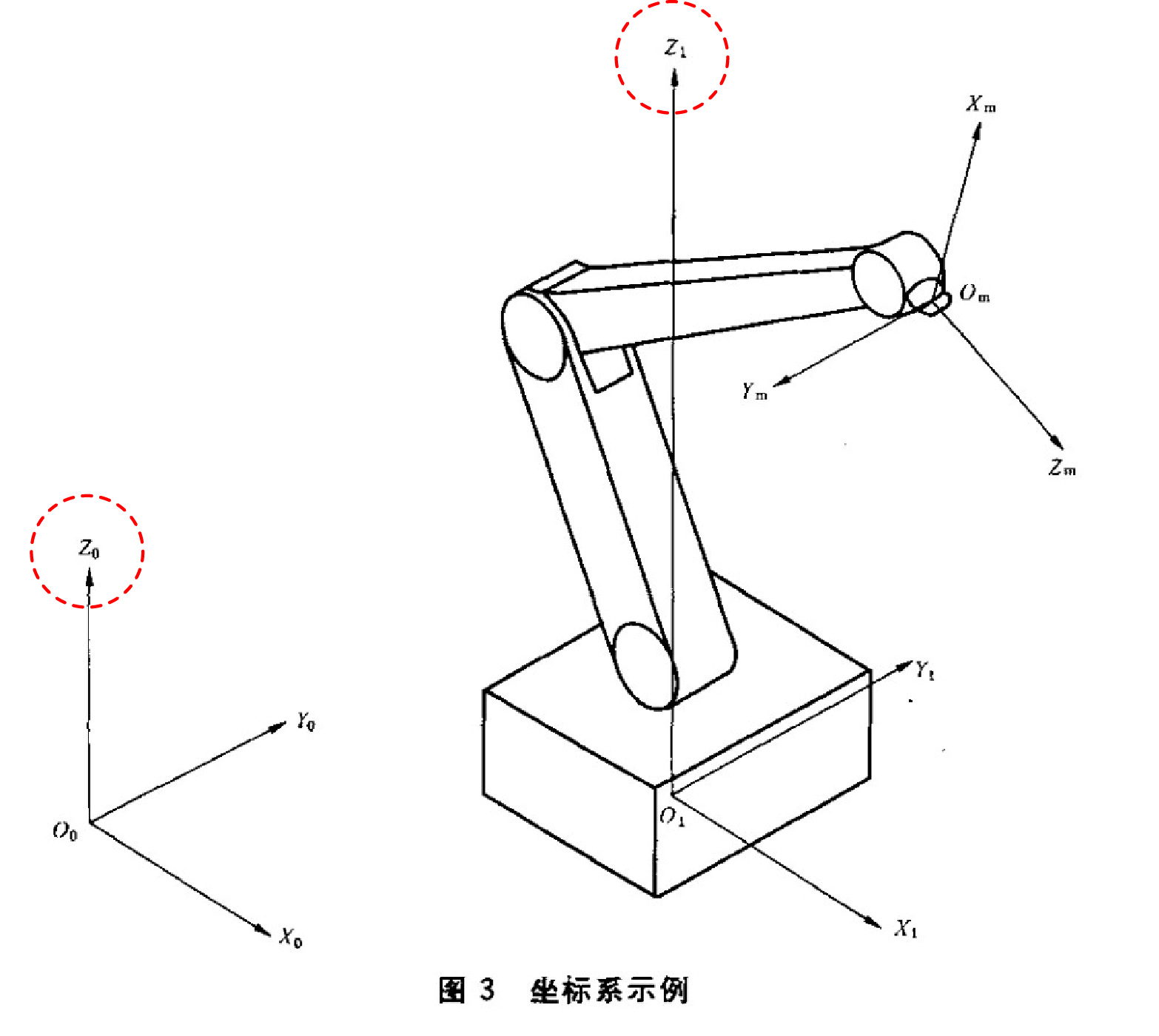
为了让机器人变成国标规定的姿势,需要旋转各个连杆。我们先想想应该怎么转:结合我们之前导入的图形,可以先绕全局坐标系的x轴转 $90^{\circ}$,再绕全局坐标系的z轴转$90^{\circ}$。还有一种方法是:先绕全局坐标系的x轴转$90^{\circ}$(记这个旋转后的坐标系为A),再绕 A的y轴转$90^{\circ}$。两种方法的效果是一样的,但是注意合成矩阵时乘法的顺序(见以下代码),不懂的同学可以看看文献[5]中的31~33页。当然,转动是有正负之分的:将你的右手握住某个坐标轴,竖起大拇指,让大拇指和轴的正方向一致,这时四指所示的方向就是绕该轴转动的正方向。
为此,我们定义旋转矩阵(两种定义效果一样):
{Xaxis,Yaxis,Zaxis}=IdentityMatrix[3]; (*定义三个旋转轴*)
rot = RotationMatrix[90 Degree, Zaxis].RotationMatrix[90 Degree, Xaxis]; (*注意第二次变换是在左边乘*)
rot = RotationMatrix[90 Degree, Xaxis].RotationMatrix[90 Degree, Yaxis]; (*注意第二次变换是在右边乘*) 然后用rot矩阵旋转每个连杆(的坐标,即保存在第一部分robotParts[[i, 1]]中的数据):
robotParts=Table[GraphicsComplex[rot.# & /@ robotParts[[i, 1]], robotParts[[i, 2]]], {i, 9}];经过姿态变换后的机器人看起来舒服点了,只是有些苍白。为了给它点个性(也方便区分不同的零件或者称为连杆),我们给连杆设置一下颜色,代码如下。你可能注意到了,这里我没有使用循环去为9个连杆一个一个地设置颜色,而是把同类的元素(颜色)写在一起,然后再和连杆列表一起转置即可把颜色“分配”给各个连杆。这样做的好处就是代码比较简洁、清晰,以后我们会经常这么做。
colors = {Gray, Cyan, Orange, Yellow, Gray, Green, Magenta, LightGreen, Pink}; (*1~9 各连杆的颜色*)
robotPartsColored = Transpose[{colors, robotParts}]; (*把颜色分配给各连杆*)
Graphics3D[robotPartsColored]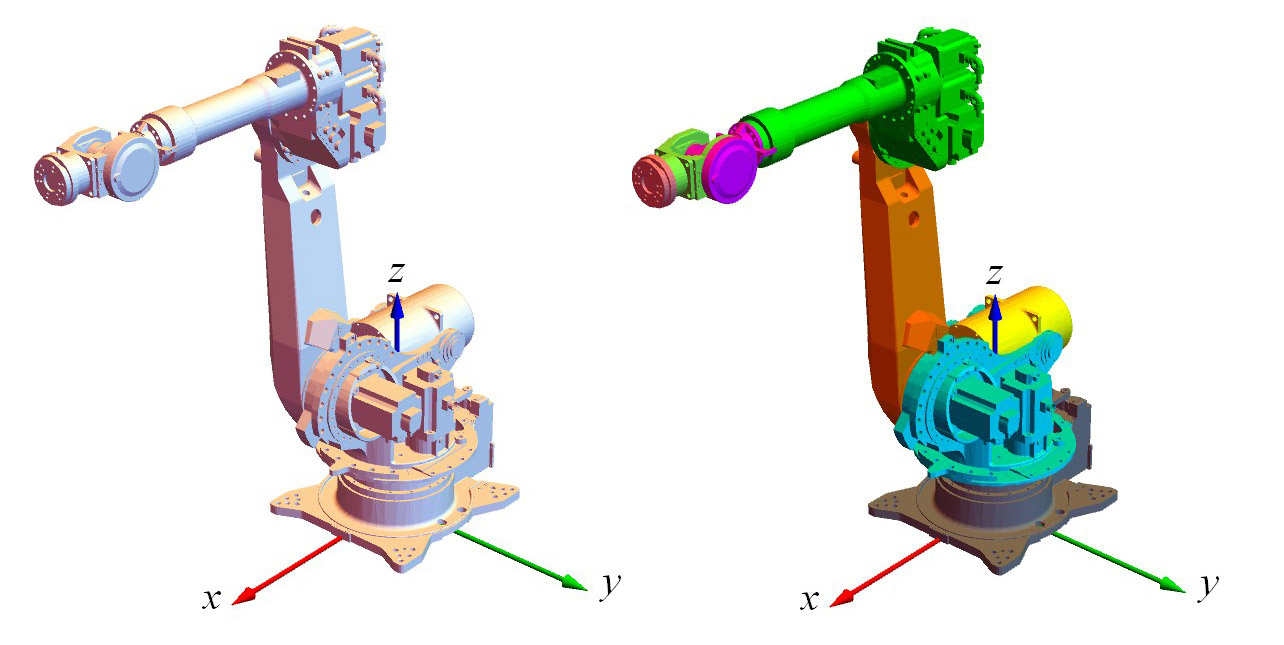
说明 现在的机器人姿势(大臂竖直、小臂前伸)是6自由度机械臂的“零位”状态,我们将此时机械臂各关节的角度认为是0。一般机械臂上都有各关节的零点位置标记,用于指示各关节的零点。我们用控制器控制机械臂时,发出的角度指令都是相对于这个零点位置的。零点位置不是必须遵守的,你可以将任意的角度设置为零位,不过为了统一,最好用机械臂固有的零位——也就是当前姿势下各关节的角度。
3. 运动学仿真
前面的工作只是让机械臂的模型显示出来。如果想让它动起来,那就要考虑运动学了。机器人这个学科听起来高大上(很多都停留在理论上),可实际上现在大多数工业机器人的控制方式还是比较低级的,它们只用到了运动学,高级一点的动力学很少用,更不要提智能了(它们要说自己有智能,我们家的洗衣机和电视机都要笑掉大牙了)。看来要使用机器人,运动学是必不可少的,所以我们先来实现运动学。
在建立运动学模型之前我们需要了解机器人的机械结构。前面提到,MOTOMAN-ES165D 是一个6自由度的串联机械臂。而6个自由度的机器人至少由7个连杆组成(其中要有一个连杆与大地固定,也就是基座)。可是我们导入的连杆有9个,多出来的2个连杆是弹簧缸(基座上黄色的圆筒)的组成部分。MOTOMAN-ES165D 机器人能够抓持的最大负载是165公斤,弹簧缸的作用就是作为配重平衡掉一部分负载的重量,要不然前端的关节电机会有很大的负担。可是弹簧缸给我们的建模造成了麻烦,因为它导致“树形拓扑”以及存在“闭链”,这不太好处理。为此,我们先忽略掉弹簧缸。
3.1 连杆的局部坐标系
机器人的运动也就是其构成连杆的运动。为了表示连杆的运动,我们要描述每个连杆的位置和姿态(合称为“位姿”)。通常的做法是在每个连杆上固定一个坐标系(它跟随连杆一起运动),这个坐标系被称为“局部坐标系”。通过描述局部坐标系的位姿我们就可以描述每个连杆的位姿。如何选择局部坐标系呢?理论上你可以任意选择,不过局部坐标系影响后续编程和计算的难易程度,所以我们在选择时最好慎重。在运动学建模和动力学建模中,坐标系的选择通常是不同的:
● 运动学建模时,连杆的局部坐标系一般放置在关节处,这是因为常用的 D-H 参数是根据相邻关节轴定义的;
● 动力学建模时,连杆的局部坐标系一般放置在质心处,这是因为牛顿方程是关于质心建立的,而且关于质心的转动惯量是常数,这方便了计算。
我们先考虑运动学,因此将局部坐标系设置在关节处。在SolidWorks中打开任何一个连杆,都能看到它自己有一个坐标系。描述一个连杆的每一条边、每一个孔的坐标都以这个坐标系为参考,我们称它为“绘图坐标系”。绘图坐标系通常不在质心处,因为在你还没画完连杆之前你根本不知道它的质心在哪里。绘图坐标系通常在连杆的对称中心或者关节处,我们不妨将每个连杆的绘图坐标系当做它的局部坐标系。
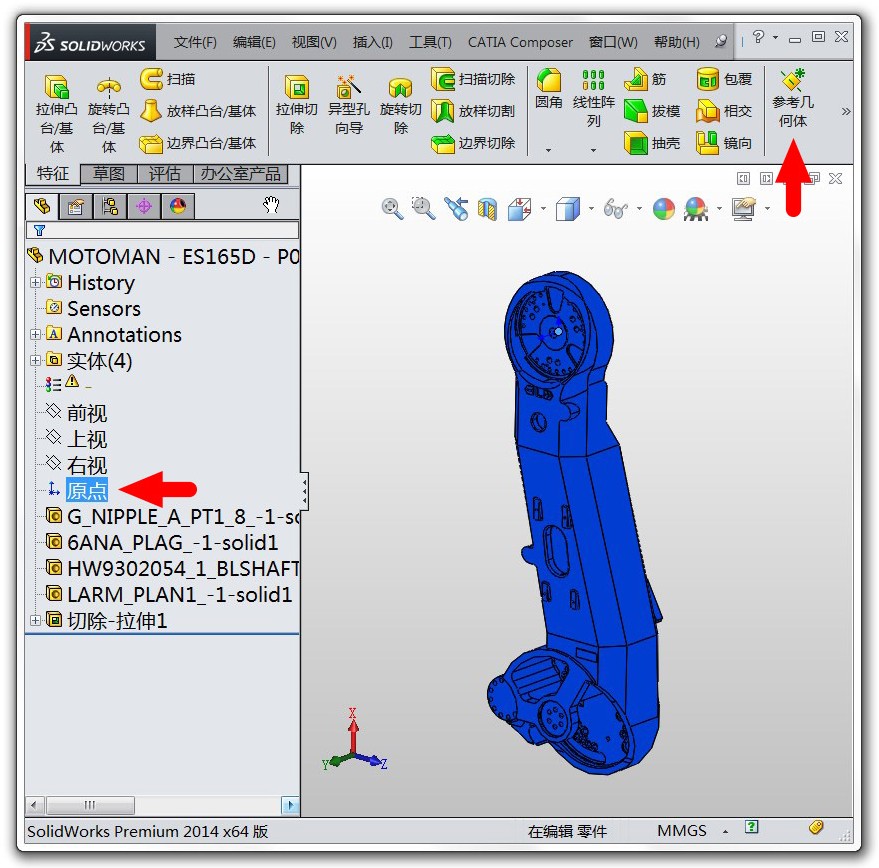
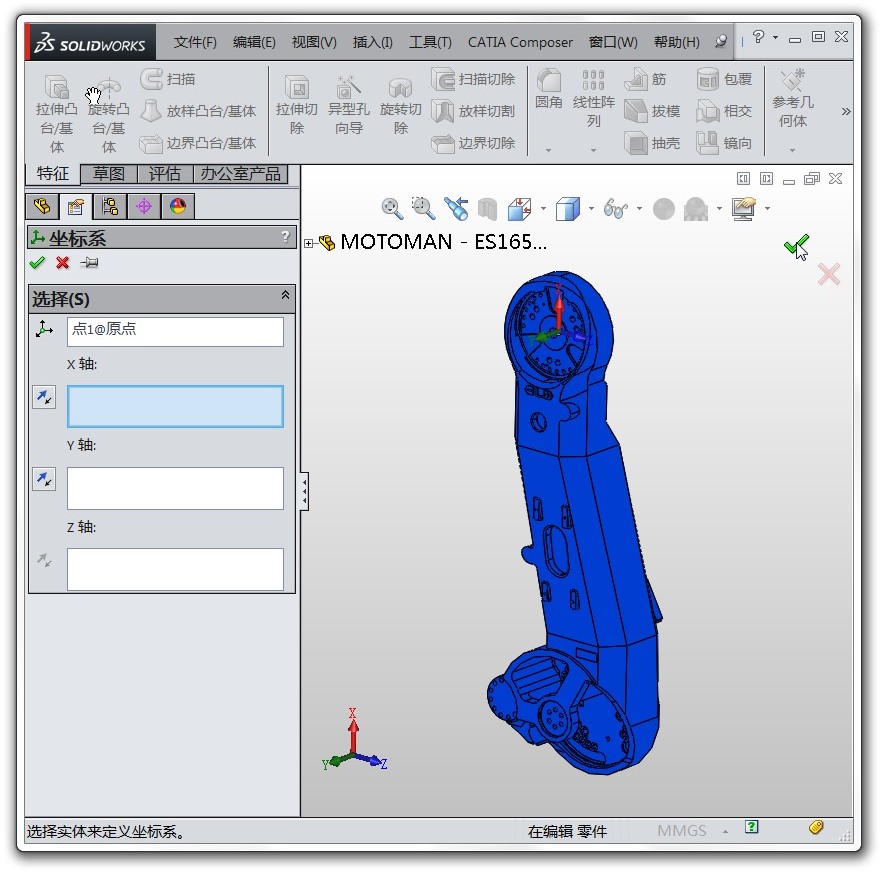
那么下一个问题是每个连杆的绘图坐标系在哪儿呢?我们以第三个连杆为例说明,如下图左所示,点击SolidWorks左侧的“原点”标签,图中就会显示绘图坐标系的原点。(如果你想将绘图坐标系显示出来,可以先选中“原点”标签,然后点击上方菜单栏中的“参考几何体”,再选择“坐标系”,然后直接回车即可看到新建的绘图坐标系,如右图,可见它位于上面的关节轴)
然后回到机器人的装配体中,在左侧的连杆树中展开每个连杆找到并选中其绘图坐标系的原点,然后点击上方菜单栏“评估”中的“测量”即可看到图中出现了一组坐标值(如下图所示),这就是连杆绘图坐标系的原点在全局坐标系(本文将全局坐标系定义为装配体的坐标系)中的位置。
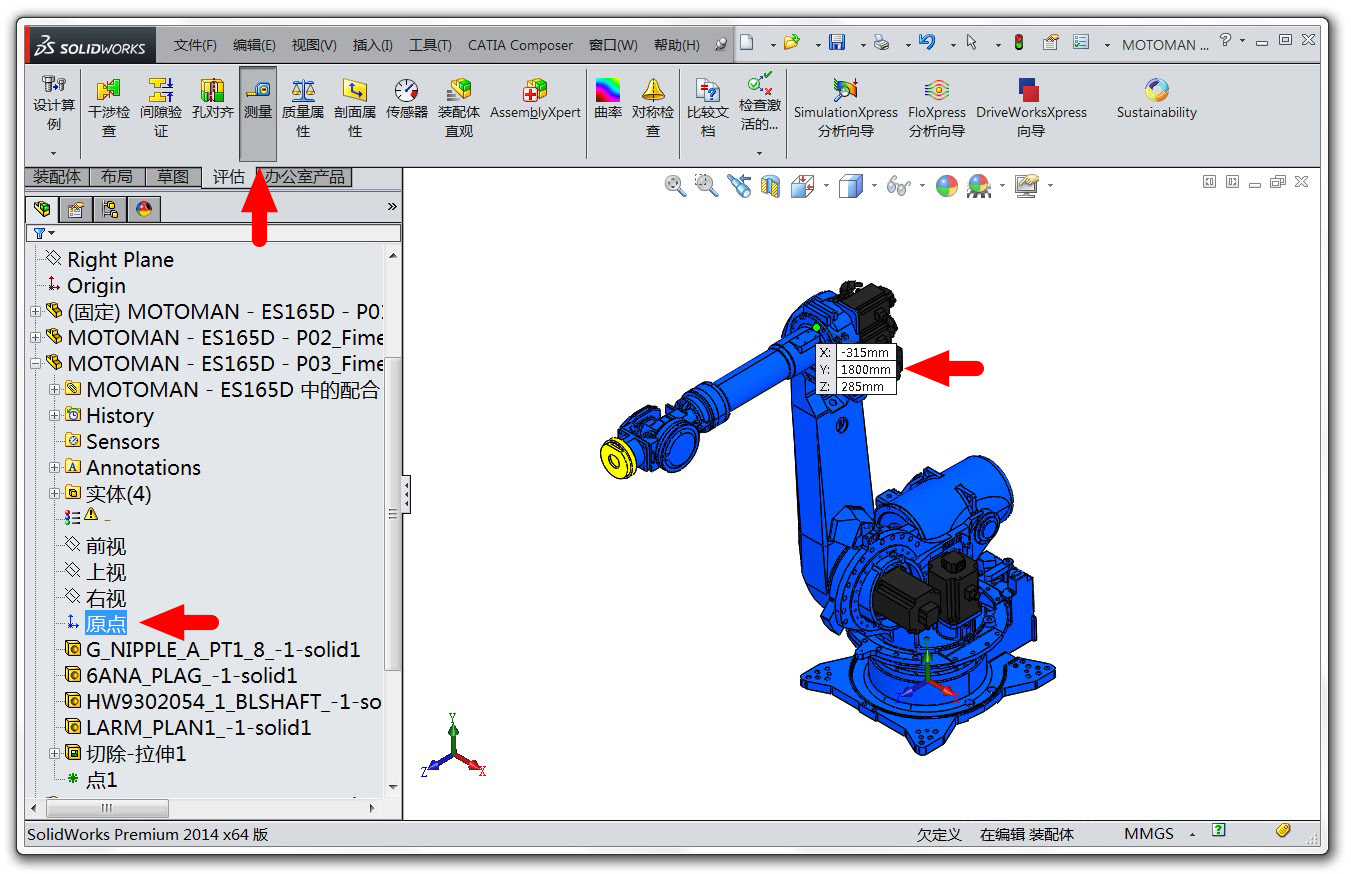
我们记录下所有连杆的绘图坐标系的原点位置(除去弹簧缸的2个,注意 SolidWorks 中默认的单位是毫米,这里除以1000是为了变换到 Mathematica 中使用的国际标准单位——米):
drawInGlobalSW = {{0, 0, 0}, {0, 650, 0}, {-315, 1800, 285}, {-53.7, 1800, 285}, {0, 2050, 1510}, {0, 2050, 1510}, {0, 2050, 1720.5}}/1000; 因为我们是在 SolidWorks 中测量的位置,所以这些位置值还是相对于 SolidWorks 的坐标系(y轴朝上),要变到z轴朝上,方法仍然是乘以旋转矩阵 rot:
drawInGlobal = Table[rot.i, {i, drawInGlobalSW}];以后我们会经常对点的坐标进行各种各样的变换(平移、旋转),而且很多时候是用一个矩阵同时对很多个点的坐标进行变换(例如上面的例子),不如定义一个算子以简化代码。我们可以定义算子(其实是一个函数):
CircleDot[matrix_,vectors_]:=(matrix.#)&/@vectors; 所以前面的变换用我们自定义的算子表示如下(复制到 Mathematica中后 \[CircleDot] 会变成一个Mathematica内部预留的图形符号$\odot$,这个符号没有被占用,所以这里我征用了):
drawInGlobal = rot\[CircleDot]drawInGlobalSW; (*哈哈!写起来是不是简单多了*)本文出现的所有自定义的函数都给出了实现代码(Mathematica 自带的函数首字母都是大写。为了与官方函数区分,我自定义的函数有些采用小写字母开头,不过建议大家采用windows编程常用的命名法,即变量名首字母小写,中间字母大写:myVariable,而函数名首字母和中间字母都大写:MyFunction)。为了方便,我将这些自定义函数打包成一个函数包,每次运行程序时导入此函数包即可使用里面的函数。注意该函数包依赖另一个函数包 Screws.m[3] ,该包基于旋量理论,可在此处下载:http://www.cds.caltech.edu/~murray/books/MLS/software.html (为了写起来省事,我修改了其中部分函数的名字,为此重新定义了 myScrews.m)。在程序中导入函数包的代码如下(如果函数包位于你的程序笔记本文件的同一目录下):
SetDirectory[NotebookDirectory[]]
<< myFunction.m 还记得吗?最开始我们导入机器人模型时,各连杆的位置都已经按照装配关系确定好了,所以它们的坐标也是相对于全局坐标系描述的。可是现在我们要让机械臂动起来(并且显示出来),这就需要移动这些坐标。为了方便起见,最好能将每个连杆的坐标表示在自己的绘图坐标系中,因为这样我们只需要移动绘图坐标系就行了,而各点的坐标相对它们所属的绘图坐标系是不动的。应该怎么做呢?很简单,将连杆的坐标减去绘图坐标系的原点在全局坐标系中的坐标即可:
partsName = {"1.stl", "2.stl", "3.stl", "6.stl", "7.stl", "8.stl", "9.stl"}; (*已经去除了组成弹簧缸的2个零件:4号和5号*)
robotPartsGraphics = Import[#, "Graphics3D"] & /@ partsName;
robotParts = robotPartsGraphics[[;; , 1]];
robotParts = Table[GraphicsComplex[rot\[CircleDot]robotParts[[i, 1]], robotParts[[i, 2]]], {i, 7}];
robotParts = Table[GraphicsComplex[(# - drawInGlobal[[i]]) & /@ robotParts[[i, 1]], robotParts[[i, 2]]], {i, 7}];
colors = {Gray, Cyan, Orange, Green, Magenta, Yellow, Pink}; (*重新定义连杆的颜色*)
robotPartsColored = Transpose@{colors, robotParts};坐标移动后的连杆如下图所示(图中的坐标系是各个连杆自己的绘图坐标系,我没有对坐标转动,所以绘图坐标系和全局坐标系的姿态相同)。我们一开始从 SolidWorks 导出文件时是一次性地导出整个装配体的。其实,如果我们挨个打开各个连杆并且一个一个的导出这些连杆,那么得到数据就是相对于各自的绘图坐标系的,只不过这样稍微麻烦一点。
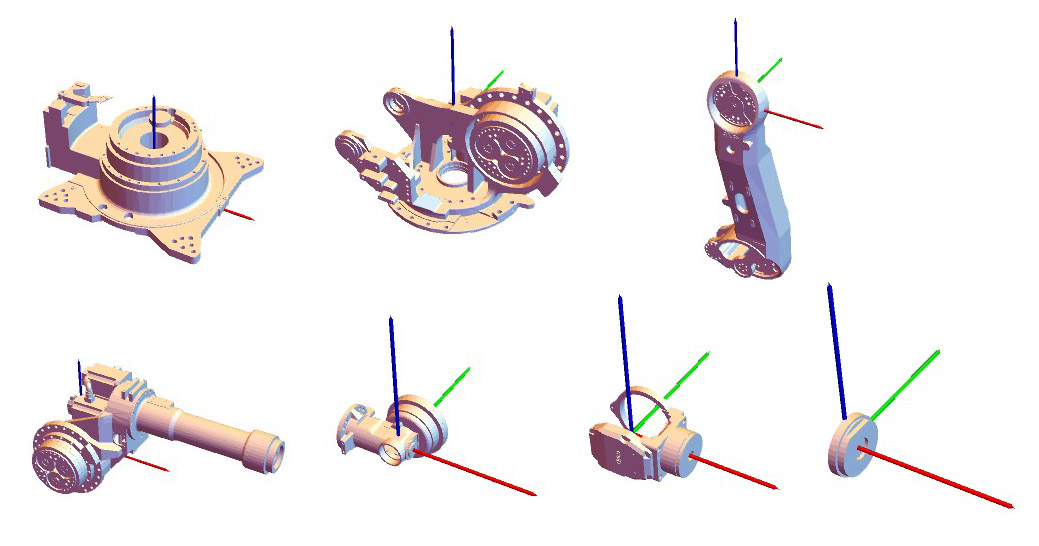
3.2 利用旋量建立运动学模型
下面我们尝试建立运动学模型。描述机器人连杆之间几何关系的经典方法是采用 D-H 参数(Denavit - Hartenberg parameters)。D-H 参数巧妙在什么地方呢?我们知道,完全确定两个坐标系(或者刚体)的位姿关系需要6个参数,因为三维空间中的刚体有6个自由度。如果不考虑关节转动(平移)仍需要5个参数。然而 D-H 参数居然只用了4个参数就能够确定相邻连杆的位姿关系,可见 Denavit 和 Hartenberg 这哥俩确实动了番脑筋。不过为了避免 D-H 参数的一些缺点,我们弃之不用而采用旋量的表示方法。刚接触旋量的同学会觉得它很难理解。听到旋量你可能会联想到螺旋,没错,螺旋运动是直线移动和旋转运动复合而成的,它是三维空间最一般的刚体运动。关于螺旋,可以看看物理学家外尔写的一本薄薄的小书《对称》。其实旋量有什么性质、它和刚体运动的关系又是什么?这些问题数学家也是用了很长时间才搞清楚。在本文中你可以把旋量简单想象成一个描述关节转动的向量。三维空间中的旋量是一个6维向量,要描述一个关节旋量需要确定一个关节轴线的方向向量(3个参数)和轴线上任意一点的坐标(又要3个参数)。
旋量和向量相似的一个地方是,对它的描述也是相对于一个坐标系的。我们选择哪个坐标系呢?这里我们要参考 D-H 参数,每一个连杆坐标系在定义时都相对于前一个连杆的坐标系。所以我们将每个关节轴的旋量表示在前一个连杆中。这次我们以2号连杆为例说明如何确定关节运动对应的旋量:
1. 首先来看关节轴线的方向,这个要相对于2号连杆的绘图坐标系。(我们要确定关节2的旋量,至于关节1的旋量最好在连杆1中确定)。从下图中看关节2的轴线方向似乎是x轴,可是我们前面将绘图坐标系的姿态和全局坐标系的姿态设定为一样的,所以应该在全局坐标系中确定,也就是y轴。
2. 关节轴线上任意一点的坐标,这个同样要相对于2号连杆的绘图坐标系。我们在轴线上任选一点即可。步骤是:点击 SolidWorks 上方菜单栏的“参考几何体”,选择“点”,然后在左侧面板选择“圆弧中心”,然后选择图中的关节轴周围的任意同心圆弧即可创建一个参考点,这个点就是我们想要的。我们可以在连杆视图中测量这个点的坐标,也可以在机器人完整装配体中测量,这里我选择后者。(测量步骤参照前面测量“连杆绘图坐标系的原点”)
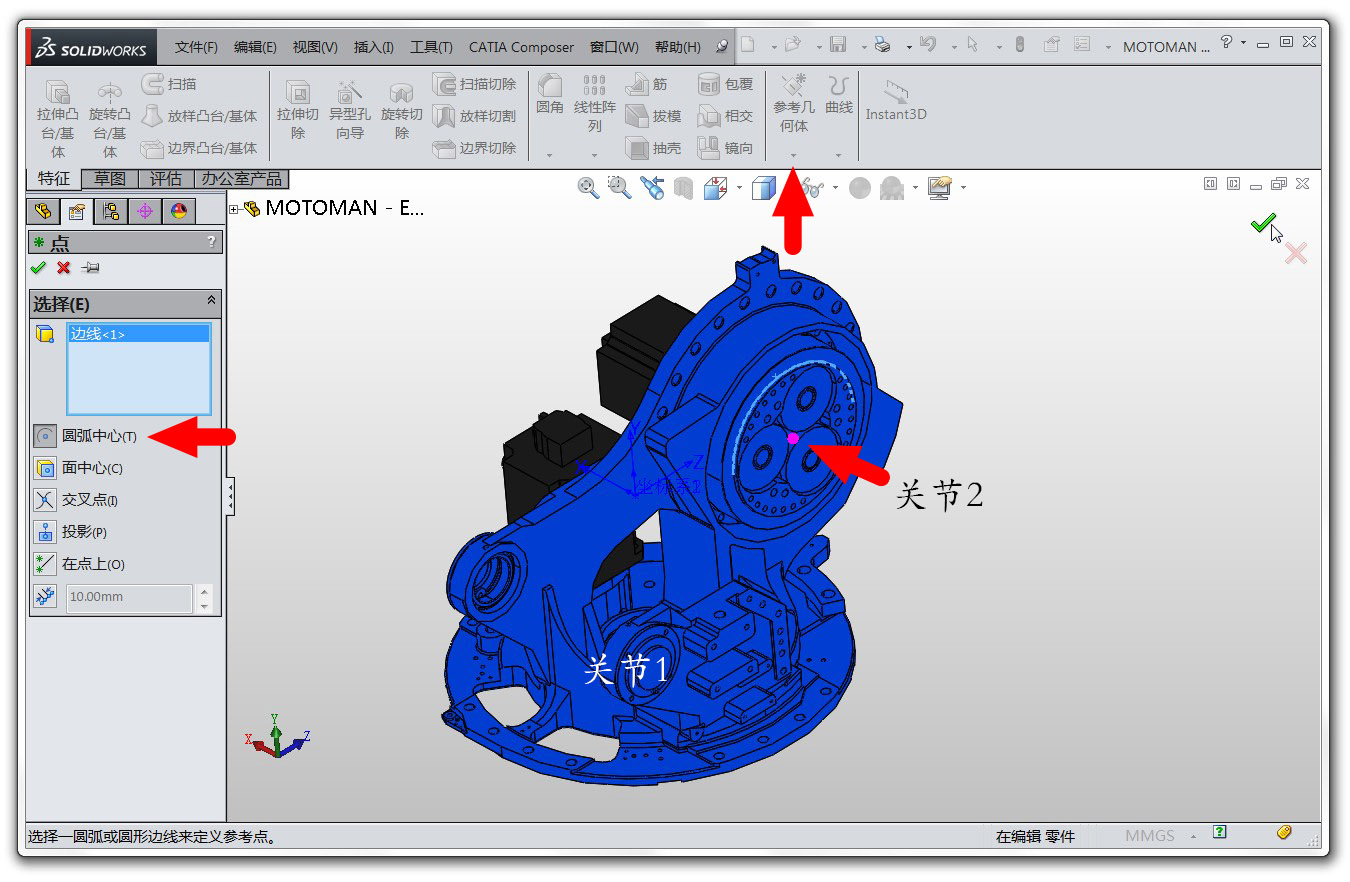
定义关节旋量的代码如下。其中相对旋量 $\xi r$ 用于迭代运动学计算,它的含义是当前连杆的转轴表示在前一个连杆坐标系中。
axesPtInGlobal = rot\[CircleDot]{{0, 257, 0}, {-88, 650, 285}, {-280.86, 1800, 285}, {0, 2050, 1318}, {134, 2050, 1510}, {0, 2050, 1720.5}}/1000;
axesPtInDraw = axesPtInGlobal - drawInGlobal[[1 ;; -2]];
axesDirInDraw = axesDirInGlobal = {Zaxis, Yaxis, Yaxis, Xaxis, Yaxis, Xaxis};
\[Xi]r = Table[\[Omega]r[i] = axesDirInDraw[[i]]; lr[i] = axesPtInDraw[[i]]; Join[Cross[-\[Omega]r[i], lr[i]], \[Omega]r[i]], {i, n}];我们对关节的相对运动进行了表示,然而要建立运动学还缺少一样东西:连杆间的初始相对位姿(初始的意思是机械臂处于“零位”的状态下)。零位下,我们将所有连杆的姿态都认为和全局坐标系一样,所以不用计算相对姿态了。至于它们的相对位置嘛,我们已经知道了绘图坐标系原点在全局坐标系中的坐标,两两相减就可以得到它们的相对位置了,很简单吧!(见下面的代码)
Do[g[L[i], L[i + 1], 0] = PToH[drawInGlobal[[i + 1]] - drawInGlobal[[i]]], {i, n}]; 其中,PToH 函数能将位置向量转换为一个$4\times4$齐次变换矩阵,这是借助 RPToH 函数实现的(RPToH 函数就是 Screws 工具包[3]中的 RPToHomogeneous 函数),它可以将一个$3\times3$旋转矩阵和$3\times1$位移向量组合成一个$4\times4$齐次变换矩阵。将旋转矩阵和位移向量合成为齐次变换矩阵是我们以后会经常用到的操作。类似的,也可以定义 RToH 函数将旋转矩阵生成对应的齐次变换矩阵,代码如下:
RToH[R_]:= RPToH[R,{0,0,0}]
PToH[P_]:= RPToH[IdentityMatrix[3],P]说明 本文中,用符号
I表示全局坐标系(同时也是惯性坐标系);符号L[i]表示第i个连杆,变量g[L[i], L[i+1]]表示第i+1个连杆相对于第i个连杆的位姿矩阵(它是一个$4\times4$齐次变换矩阵);变量g[I, L[i]]表示什么你肯定猜到了,它表示第i个连杆相对于全局坐标系的位姿矩阵。如果不特别说明,本文总是用g(或者g开头的变量)表示一个(或一组)齐次变换矩阵,这是约定俗成的。
现在可以正式推导机械臂的运动学模型了。在使用机械臂时,大家一般只关心其最末端连杆的位姿,更确切的说,是最末端连杆的位姿与关节角度的关系。不过为了得到最末端连杆的位姿,我们需要计算中间所有连杆的位姿。这里利用相邻连杆的迭代关系——每个连杆的位姿依赖前一个连杆的位姿——来提升计算效率。所以,可以定义机械臂所有连杆的运动学函数为:
robotPartsKinematics[configuration_] := Module[{q, g2To7},
{g[I, L[1]], q} = configuration;
g2To7 = Table[g[L[i], L[i + 1]] = TwistExp[\[Xi]r[[i]], q[[i]]].g[L[i], L[i + 1], 0];
g[I, L[i + 1]] = g[I, L[i]].g[L[i], L[i + 1]], {i, n}];
Join[{g[I, L[1]]}, g2To7] ] robotPartsKinematics函数的输入是:基座的位姿矩阵 g[I, L[1]] 和所有关节的角度向量q$\in\mathbb{R}^{6}$,这组变量完整地描述了一个串联机械臂的位置和姿势(用机器人中的专业术语应该叫“构型”: configuration,注意不要翻译为“配置”),而输出则是所有连杆相对于全局坐标系的$4\times4$位姿矩阵(即 g[I, L[i]],其中i = 1~7)。
其中,TwistExp 函数来自于 Screws 工具包[3],作用是构造旋量的矩阵指数。
在大多数的机器人教科书中,连杆的记号是从0开始的,也就是说将基座记为0号连杆,然后是1号连杆,最末端的连杆是n+1号(假设机械臂的自由度是n);而关节的记号是从1开始,也就是说1号关节连接0号连杆和1号连杆。这样标记的好处是记号一致,推导公式或编程时不容易出错:比如说我们计算第i个连杆的速度时要利用第i个关节的转动速度。可是本文中连杆的记号是从1开始的(基座标记为1号连杆),我们保留0号标记是为了以后将机械臂扩展到装在移动基座(比如一个AGV搬运小车)的情况,这时0号就用来表示移动基座。
可以看到,只要定义好关节旋量,建立运动学模型非常简单。可是这样得到的运动学模型对不对呢?我们来检验一下。借助 Manipulate 函数,可以直接改变机械臂的各关节角度,并直观地查看机械臂姿势(应该叫构型了哦)的变化,如以下动画所示。可以看到,机械臂各连杆的运动符合我们设置的关节值,这说明运动学模型是正确的。

Manipulate[q = {##}[[;; , 1, 1]];
gs = robotPartsKinematics[{IdentityMatrix[4], q}];
Graphics3D[{MapThread[move3D, {robotPartsColored, gs}]}
, PlotRange -> {{-2, 3}, {-2, 3}, {0, 3}}], ##, ControlPlacement -> Up] & @@ Table[{{qt[i], 0}, -Pi, Pi, 0.1}, {i, n}]move3D[shape_,g_]:=GeometricTransformation[shape,TransformationFunction[g]] 验证使用的代码如上。其中,move3D 函数的功能是用一个齐次变换矩阵(g)移动一个几何图形(shape)。这里还值得一提的是 MapThread 函数。虽然我们可以用 move3D 函数去一个一个地移动连杆(写起来就是:move3D[part1, g1], move3D[part2, g2], move3D[part3, g3]),这样写比较清楚也很容易读懂,可就是太麻烦了。如果你的机械臂有一百个连杆,用这种方法岂不是要累死。当然,我们可以使用循环,但是使用 MapThread 函数写起来更简单,即:MapThread[move3D, {{part1, part2, part3}, {g1, g2, g3}}],而且得到的结果与前面完全一样。这就是为什么我喜欢把同类型的元素都放到一起,因为操作的时候可以一起批量化进行,使得代码更简洁。
可以看到,Mathematica 提供的控件类函数 Manipulate 支持用户使用鼠标交互式地改变变量的值,同时动态更新对应的输出。如果一段代码运行时间足够快,就可以放在Manipulate 内部,比如运动学函数robotPartsKinematics,它包含的计算并不复杂,但如果是后面要介绍的动力学函数就不适合放在Manipulate里面了,因为动力学的计算比较耗时,窗口会显得很“卡顿”。
随着对 Mathematica 越来越熟悉,你会逐渐体会到它的强大。比如说你可以随心所欲地将已有的函数组合从而得到新的函数,如果一段代码被频繁地使用我们就可以这么干。举个例子,我们可以借助robotPartsKinematics来定义一个新的函数robotMoveToQ,用来得到某个构型下的机械臂的外观:
robotMoveToQ[q_] := Module[{gs},
gs = robotPartsKinematics[{IdentityMatrix[4], q}];
MapThread[move3D, {robotPartsColored, gs}] ]而且,函数的使用也很灵活。例如,我们可以将不同构型下的机械臂同时显示出来,只需要两行代码,如下:
qs = Table[{a - Pi/2, a/2, -a/2 + Pi/6, 0, 0, 0}, {a, 0, Pi, 0.2}];(*生成关节变量列表,即不同构型*)
Graphics3D[{robotMoveToQ /@ qs}]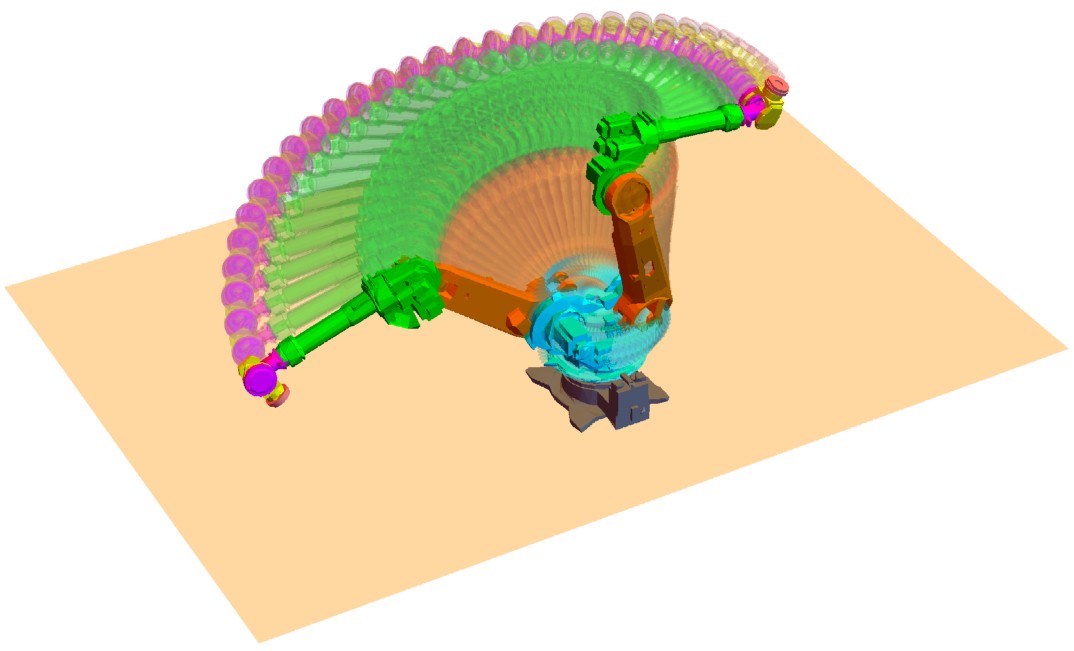

4. 逆运动学仿真
借助运动学,我们成功地通过改变关节角度实现了对机械臂的控制。当然这没什么值得炫耀的,本质上不过是矩阵相乘罢了。本节我们考虑一个更有挑战性也更好玩的问题。如果告诉你所有连杆(局部坐标系)的位姿,你能不能算出机械臂的各个关节角来?你一定会说这很简单,求一下反三角函数就行了。但是实际应用时经常会遇到比这个难一些的问题:只告诉你机械臂最后一个连杆的位姿,如何得到各关节的角度?这个问题被称为“逆运动学”。Robotic Toolbox工具箱[2]中给出了两个解逆运动学问题的函数:ikine 和 ikine6s,分别是数值解法和符号解析解法,本文我们也用两种方式解决逆运动学问题。
4.1 数值解法之——解方程
上一节的运动学函数 robotPartsKinematics 能得到所有连杆的位姿。大多数时候,人们只关心最后一个连杆的位姿(因为它上面要装载操作工具),即 Last@robotPartsKinematics[{IdentityMatrix[4], q}](注意q是一个六维向量,即q=$(q_1,q_2,q_3,q_4,q_5,q_6)$),结果如下图所示(另存为可以看大图)。这里关节角没有设置数值,因此得到的是符号解,有些长哦。这也是为什么机器人领域经常使用三角函数缩写的原因:比如把 $\cos(q_1)$记为$c_1$。在[4]中提供了一个函数 SimplifyTrigNotation,可以用来对下式进行缩写。
如果我们想让机械臂末端(连杆)到达某个(已知的)位姿 gt,也就是让上面的矩阵等于这个位姿矩阵:
Last@robotPartsKinematics[{IdentityMatrix[4], {q1, q2, q3, q4, q5, q6}}] = gt (*逆运动学方程*) 通过解上面这个以6个关节角 $(q_1,q_2,q_3,q_4,q_5,q_6)$ 为未知量的方程组就能知道机械臂的构型了。也就是说,逆运动学问题的本质就是解方程。对于解方程我们一点也不陌生,从小到大我们解过无数的方程。甚至可以说数学这个学科本身有很大一部分就是在研究解方程、解各种各样的方程:大规模的、小规模的,线性的、非线性的,代数的、微分的,常微分的、偏微分的。既然有这么多种方程,也就意味着存在很多种解法。Mathematica 提供的用来解方程的函数不止一个,例如有:Solve、NSolve、DSolve、LinearSolve、FindRoot 等等。面对这么多解方程的工具,我们应该选哪个呢?你选择的函数取决于方程的类型,所以我们先看看这个方程是什么类型呢?首先,它是个代数方程,所以不能使用求解微分方程的函数(DSolve)。其次,方程中包含未知量的三角函数,所以它是非线性代数方程,因此不能用求解线性方程的函数(LinearSolve)。再者,对于代数方程有数值解法和解析解法两类方法。当然,我们非常想得到用符号表示的解析解,因为只需要解一次以后直接带入数值即可,计算速度非常快。但是非线性方程一般很难得到符号解(对于这个机械臂,它存在符号解),所以我们只好退而求其次寻找数值解了,这样就把范围缩小到 NSolve、FindRoot 这两个函数了。NSolve 会得到所有解(这个方程有不止一组解哦),而 FindRoot 会根据初始值得到最近的解。一番试验表明只有 FindRoot 能满足要求。
在求解逆运动学方程前还需要解决一个小问题:如何在 Mathematica 中表示一个期望的目标位姿
gt呢?Mathematica 提供了RollPitchYawMatrix函数和EulerMatrix函数用来表示三维转动(你用哪个都可以),然后利用前面的RPToH函数合成为位姿矩阵gt即可,示例代码如下。其中,cuboid函数用于绘制一个长方体。如果你使用 Matlab ,那我要可怜你了。因为 Matlab 没有绘制长方体的函数,一切你都要自己画。 而 Mathematica 定义了一些常用几何图形,可以直接用。
cuboid[center_, dim_]:= Cuboid[center - dim/2, center + dim/2]; (*输入center是长方体的几何中心,dim是长方体的长宽高*)object = cuboid[{0, 0, 0}, {0.3, 0.2, 0.05}];
Manipulate[
gt = RPToH[EulerMatrix[{\[Alpha], \[Beta], \[Gamma]}], {x, y, z}];
Graphics3D[{Yellow, move3D[{frame3D, object}, gt]}, PlotRange -> 0.5], Grid[{{Control[{{x, 0}, -0.5, 0.5, 0.01}], Control[{{\[Alpha], 0}, -Pi, Pi, 0.1}]}, {Control[{{y, 0}, -0.5, 0.5, 0.01}],Control[{{\[Beta], 0}, -Pi, Pi, 0.1}]}, {Control[{{z, 0}, -0.5, 0.5, 0.01}], Control[{{\[Gamma], 0}, -Pi, Pi, 0.1}]}}], TrackedSymbols :> True]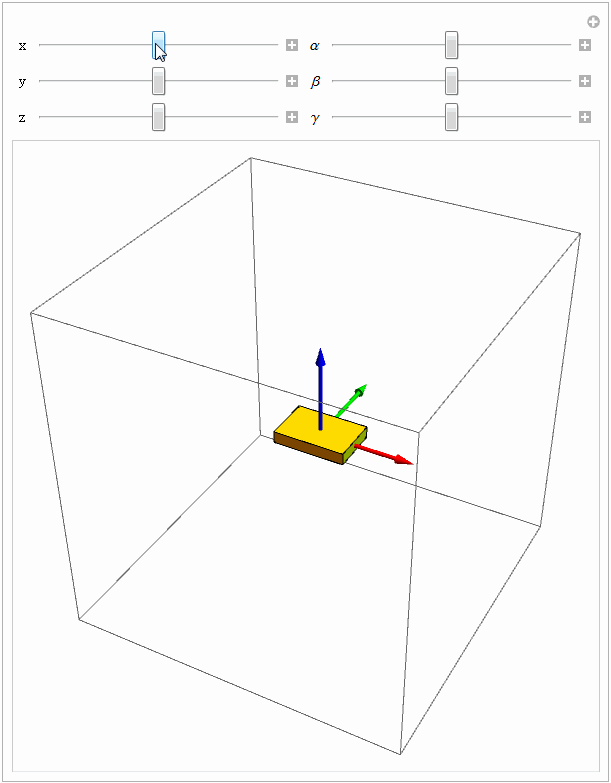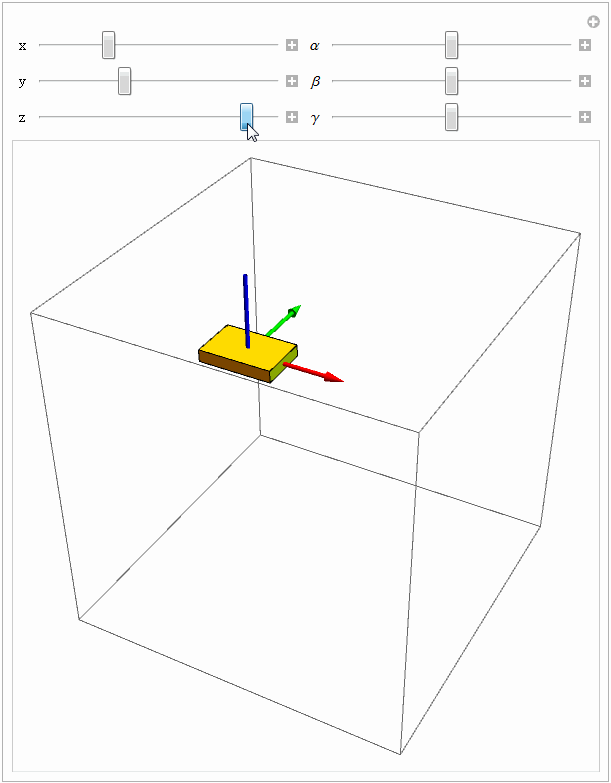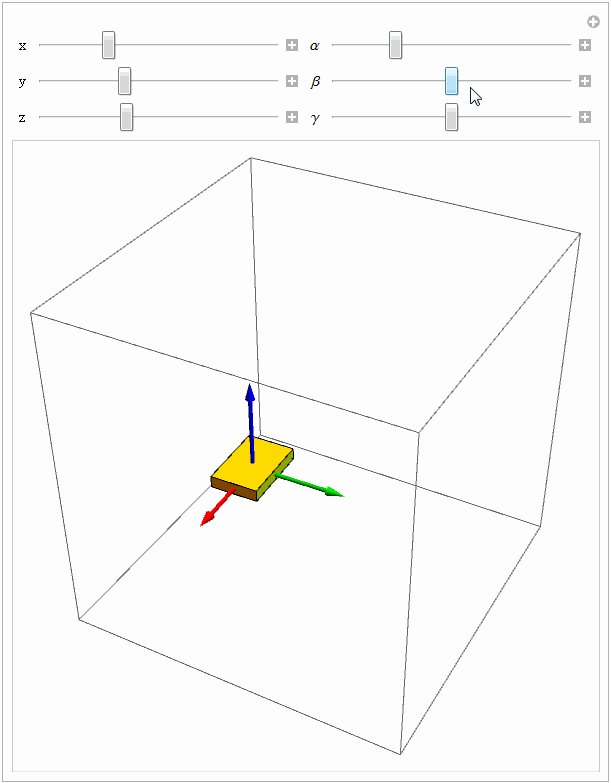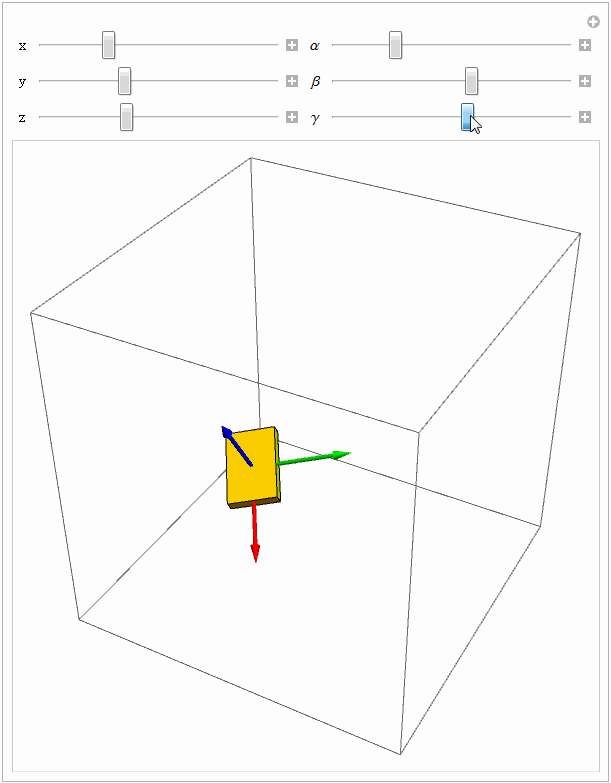
不过这个方程组是由 $4\times4$ 齐次变换矩阵得到的,里面有$4\times4 =16$个方程,去掉最后一列(0,0,0,1)对应的4个恒等式还有12个方程,超过了未知量(6个)的个数,这是因为 $3\times3$ 旋转矩阵的各项不是独立的,因此要舍去一部分。该保留哪三项呢?只要不选择同一行或同一列的三项就可以了,这里我保留了(1,2),(2,3),(3,3)三项(但不是全都对,有时你需要试试其它项)。
Manipulate[
gts = Last@robotPartsKinematics[{IdentityMatrix[4], {q1, q2, q3, q4, q5, q6}}];
gt = RPToH[RollPitchYawMatrix[{\[Alpha], \[Beta], \[Gamma]}], {x, y, z}];
Quiet[q = {q1, q2, q3, q4, q5, q6}/.FindRoot[gts[[1, 4]] == gt[[1, 4]] && gts[[2, 4]] == gt[[2, 4]] && gts[[3, 4]] == gt[[3, 4]] && gts[[1, 2]] == gt[[1, 2]] && gts[[2, 3]] == gt[[2, 3]] && gts[[3, 3]] == gt[[3, 3]], {q1, 0}, {q2, 0}, {q3, 0}, {q4, 0.3}, {q5, 0.3}, {q6, 0.3}]];
planeXY = {FaceForm[], EdgeForm[Thickness[0.005]], InfinitePlane[{x, y, z}, {{0, 1, 0}, {1, 0, 0}}], InfinitePlane[{x, y, z}, {{0, 1, 0}, {0, 0, 1}}]};
lines = {Red, Thickness[0.0012], Line[{{x, y, z} + {100, 0, 0}, {x, y, z} + {-100, 0, 0}}], Line[{{x, y, z} + {0, 100, 0}, {x, y, z} + {0, -100, 0}}], Line[{{x, y, z} + {0, 0, 100}, {x, y, z} + {0, 0, -100}}]};
Graphics3D[{planeXY, lines, robotMoveToQ[q], move3D[frame3D, g[I, L[7]]]}, PlotRange -> {{-1.5, 2.5}, {-2.5, 2.5}, {0, 3}}],
Grid[{{Control[{{x, 1.3}, -2, 3, 0.1}], Control[{{y, 0}, -2, 2, 0.1}]},
{Control[{{z, 2}, 0, 3, 0.1}], Control[{{\[Alpha], 0}, 0, Pi, 0.1}]},
{Control[{{\[Beta], 0}, 0, Pi, 0.1}], Control[{{\[Gamma], 0}, 0, Pi, 0.1}]}}], TrackedSymbols :> True] 同样借助 Manipulate 函数改变值的大小,试验的效果见下图。
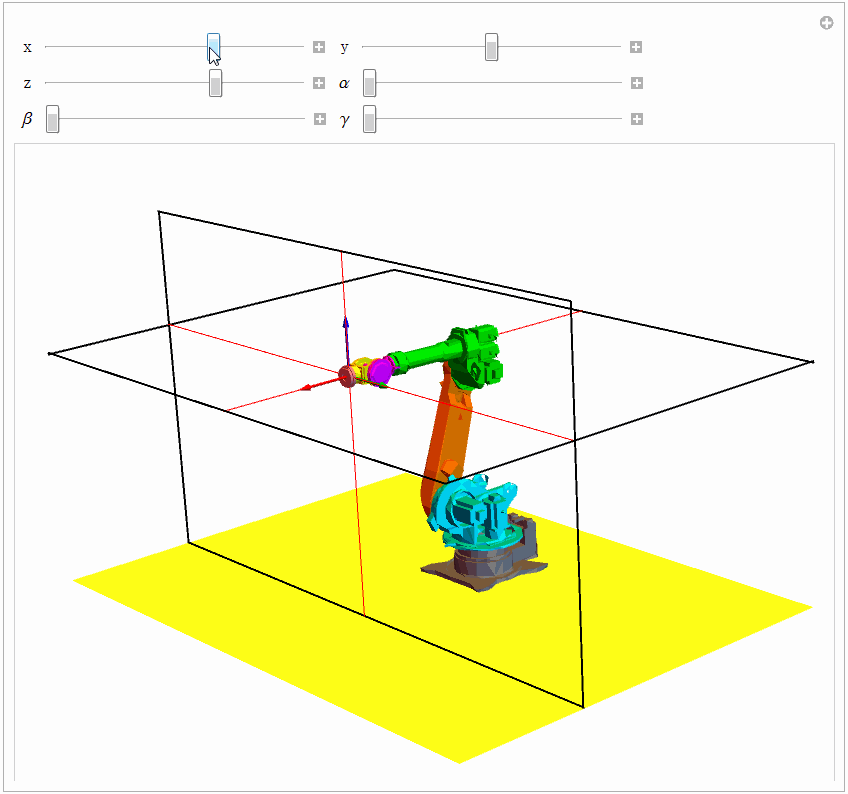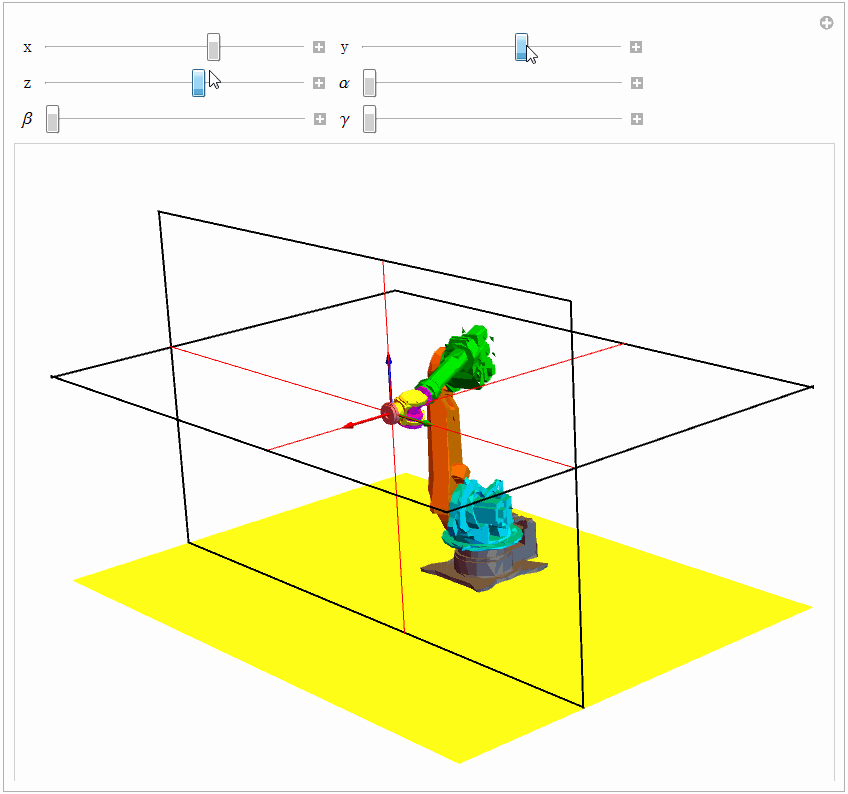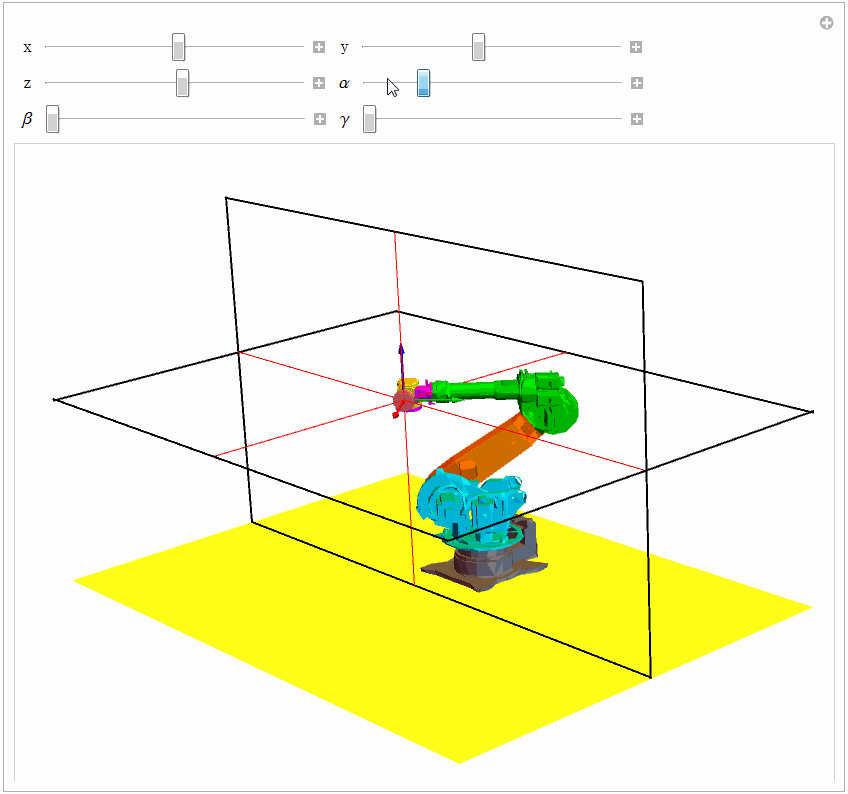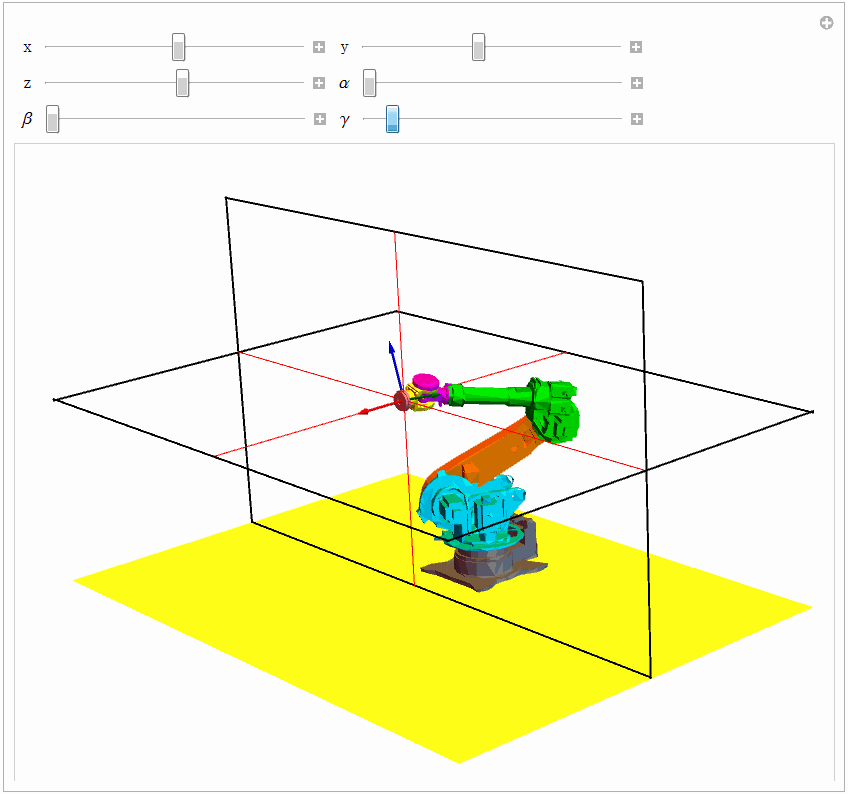
4.2 数值解法之——迭代法
解方程的方法很多,下面我们换一种思路求解逆运动学方程,其思想来自于[2](英文版187页),代码如下:
forwardKinematicsJacobian[argList_, gst0_] :=
Module[{g = IdentityMatrix[4], \[Xi], n = Length[argList]},
Js = {}; (*注意空间雅可比矩阵Js是全局变量,后面会用*)
Do[\[Xi] = Ad[g].argList[[i, 1]];
Js = Join[Js, {\[Xi]}];
g = g.TwistExp[argList[[i, 1]], argList[[i, 2]]]
, {i, n}];
Js = Transpose[Js];
g.gst0 ]
\[Xi]a = Table[\[Omega]a[i] = axesDirInGlobal[[i]]; la[i] = axesPtInGlobal[[i]]; Join[Cross[-\[Omega]a[i], la[i]], \[Omega]a[i]], {i, n}];
(*forwardKinematicsJacobian函数是从 Screws.m 中抄的,它使用的旋量都要求表示在全局坐标系中,因此需要定义绝对旋量\[Xi]a*)
inverseKinematics[gt_, q0_, errorthreshold_: 0.0001] :=
Module[{gReal, q = q0, Jb, Jg, F, error, theta, axis, positionerror, angleerror, maxIter = 20},(*输入期望的机械臂末端位姿 gt 和初始关节角 q0*)
Do[gReal = forwardKinematicsJacobian[Transpose@{\[Xi]a, q}, g[I, L[7], 0]];
Jb = Ad[Inverse[gReal]].Js;
Jg = diagF[HToR[gReal], HToR[gReal]].Jb;
positionerror = HToP[gt - gReal];
angleerror = Reverse@RollPitchYawAngles[HToR[gt.Inverse[gReal]]]; (*注意Reverse函数*)
error = Flatten[N[{positionerror, angleerror}]]; (*误差向量 error 包括位置和角度分量在全局坐标系中表示*)
F = PseudoInverse[Jg].error;
q = q + modToPiPi[F];
If[Norm[error] < errorthreshold, Break[]]
,{maxIter}];
q] 函数forwardKinematicsJacobian 用于计算(空间)雅可比矩阵和最后一个连杆的位姿,它修改自 Screws 工具包[3]。逆运动学计算函数 inverseKinematics 的输入是期望的末端连杆位姿 gt,迭代的初始角度 q0 ,以及误差阈值 errorthreshold (默认值为 0.0001)。
其中的 modToPiPi 函数(实现代码如下)用于将角度值转换到 $-\pi\sim\pi$ 的范围之间。这里为什么需要 modToPiPi 函数呢?因为角度是个小妖精,如果我们不盯紧它,它可能会时不时的捣乱。从外部看,机械臂的一个转动关节位于角度 $\pi/3$ 和角度 $\pi/3+2\pi$ 没什么区别。可是如果我们放任角度这样随意跳变,会导致轨迹不连续,这样机械臂在跟踪轨迹时就会出现麻烦。
modToPiPi[angle_]:= Module[{a = Mod[angle,2.0*Pi]}, If[Re[a]>=Pi, a-2.0*Pi, a]]
SetAttributes[modToPiPi,Listable]; 其中,Ad 函数就是 Screws 工具包[3]中的 RigidAdjoint 函数,它表示一个齐次变换矩阵的伴随变换(Adjoint Transformation),diagF 函数用于将多个矩阵合成为块对角矩阵,实现代码如下:
diagF=SparseArray[Band[{1,1}]->{##}]& (*用法为 A = {{1,2},{3,4}}; B = {{5,6},{7,8}}; diagF[A,B]//MatrixForm *) HToR 函数和 HToP 函数分别用于从一个齐次变换矩阵中取出旋转矩阵(R)和位移向量(P),代码如下。
HToR[g_]:= Module[{n=(Dimensions[g])[[1]]-1}, g[[1;;n,1;;n]]]
HToP[g_]:= Module[{n=(Dimensions[g])[[1]]-1}, g[[1;;n,n+1]]]我们以后会用到很多矩阵操作(比如转置、求逆),而 Mathematica 的函数名太长,为了写起来方便,我定义了简写的转置和求逆函数,代码如下:
T[g_]:=Transpose[g]
Iv[g_]:=Inverse[g]我们想让机械臂(的末端)依次到达一些空间点(这些点可能是机械臂运动时要经过的)。为此首先生成一些三维空间中的点:
Clear[x,y];
pts2D = Table[{Sin[i], Cos[i]}/1.4, {i, 0, 4 Pi, Pi/400}]; (*先生成二维平面上的点,它们均匀地分布在一个圆上*)
pts3D = pts2D /. {x_, y_} -> {1.721, x, y + 1.4}; (*再将二维坐标变换成三维坐标*)
Graphics3D[Point[pts3D]] 然后调用逆运动学函数 inverseKinematics 挨个计算不同点处的关节值,代码如下:
gStars = PToH /@ pts3D; (*将三维点的坐标转换成齐次变换矩阵,转动部分始终不变*)
q = ConstantArray[0, n]; (*inverseKinematics函数包含一个迭代过程,因此需要提供一个初始值*)
g[I, L[7], 0] = (robotPartsKinematics[{IdentityMatrix[4], q}]; g[I, L[7]]); (*forwardKinematicsJacobian函数需要零位状态下的末端连杆位姿*)
qs = Table[q = inverseKinematics[gt, q], {gt, gStars}]; (*依次遍历所有点,我们用每次计算得到的 q 作为下一次迭代的初始值,这样迭代速度更快*) 计算结果 qs 中存储了机械臂到达不同点处的关节向量,如果以后我们想让机械臂跟踪这个向量序列,可以对其插值得到连续的关节函数,这是靠 Interpolation 函数实现的,代码如下。关于 Interpolation 函数我要啰嗦几句,因为以后我们可能会经常用到它。对于机械臂的每个关节来说, Interpolation 得到的是一个插值函数(InterpolatingFunction),更确切地说是“Hermite多项式” 或“Spline 样条”插值函数。插值函数与其它的纯函数没什么区别,比如说我们可以对它求导、求积分。对这6个关节的插值函数求导就能得到关节速度和加速度函数:
time = 10; (*time是自己设置的,表示机械臂运动经过所有点的总时间*)
Do[qt[i] = T@{Range[0, time, time/(Length[(T@qs)[[i]]] - 1)], (T@qs)[[i]]}, {i, n}];
Do[qfun[i] = Interpolation[qt[i]];
dqfun[i][x_] = D[qfun[i][x], x];
ddqfun[i][x_] = D[dqfun[i][x], x], {i, n}]画出插值后各关节的角度、角速度、角加速度的变化趋势,如下图。能看到有两个关节角速度变化剧烈,因此,理论上这个曲线不适合让机器人跟踪。
pq = Plot[Evaluate@Table[qfun[i][x], {i, n}], {x, 0, time}, PlotRange -> All];
pdq = Plot[Evaluate@Table[dqfun[i][x], {i, n}], {x, 0, time}, PlotRange -> All];
pddq = Plot[Evaluate@Table[ddqfun[i][x], {i, n}], {x, 0, time}, PlotRange -> All];
GraphicsGrid[{{pq, pdq, pddq}}]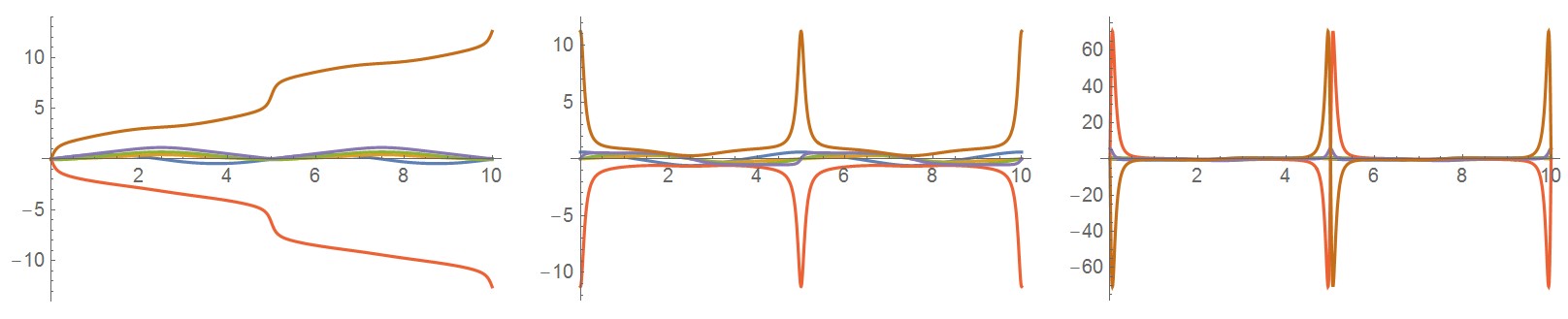
4.3 雅克比矩阵的零空间
在上一节求解逆运动学问题时我们使用了机械臂的雅克比矩阵,它能够将关节速度映射到末端连杆的速度。由于末端连杆的速度有不止一种定义方式(例如有:空间速度、本体速度、全局速度,它们的定义见我的另一篇博客),所以对应了不同的雅克比形式(也就是逆运动学函数中的 Js、Jb、Jg)。
雅克比矩阵是机器人学里的“红人”,它出现在很多场合,在这个圈子混的时间长了你经常能见到它。雅克比矩阵有一些有趣的性质,比如它的零空间。只要机械臂的关节速度在其雅克比矩阵的零空间中,那么末端连杆的速度总是零,零空间由此得名。通俗的说就是:不管关节怎么动,末端连杆始终不动(就像被钉死了一样)。这个性质还挺有用的,因为有些场合要求机械臂在抓取东西的时候还能躲避障碍物。在其它领域,例如摄影,为了保证画面稳定需要摄像机能防抖动;在动物王国中,动物觅食时头部要紧盯猎物(被恶搞的稳定鸡);在军事领域(例如坦克、武装直升机),要求炮口始终瞄准目标,不管车身如何移动和颠簸。


对于本文中的 6 自由度机械臂,由于它不是冗余的,所以大多数时候计算零空间会得到空(也就是说不存在零空间)。为了形象地展示零空间的效果,我不得已只用了平移的部分。以下代码展示了机械臂在(平移)零空间中的一种运动,如下图所示。可以看到,不管机械臂如何运动,末端连杆(局部坐标系)的位置始终不动(但是它的姿态会改变,矩阵mask 的作用就是滤掉转动分量,只剩下沿 $x、y、z$ 轴的平移运动)。BodyJacobian 函数用于计算本体雅可比矩阵,它也来自于 Screws 工具包[3]。零空间是个线性空间,如果我们知道它的一组基向量,通过线性组合能够得到任意的(速度)向量。NullSpace函数返回的刚好就是构成矩阵的零空间的一组基向量。通过对这组基向量线性组合即可得到速度向量,其使机械臂末端始终不动。下面的例子中使用的组合系数都是 1 ,也就是所有基向量相加(向量相加就是对应元素相加,由Total函数完成)。由于雅可比矩阵是机械臂构型q的函数,所以机械臂的构型一旦改变了,我们就要重新计算它的雅可比矩阵。如果还不理解,可以随时显示出dq的值,然后计算Jgm.dq看看结果是不是零。如果是零就说明dq在零空间里。
q = ConstantArray[0, n];
dt = 0.05;
g[I, L[7], 0] = Last@robotPartsKinematics[{IdentityMatrix[4], q}];
{xl, yl, zl, xr, yr, zr} = IdentityMatrix[6];
mask = {xl, yl, zl};
Animate[Jb = BodyJacobian[T@{\[Xi]a, q}, g[I, L[7], 0]];
gIL7 = Last@robotPartsKinematics[{IdentityMatrix[4], q}];
Jg = diagF[HToR[gIL7], HToR[gIL7]].Jb;
Jgm = mask.Jg;
dq = Total[NullSpace[Jgm]]; (*速度定义为零空间的一种线性组合方式,你可以试试其它线性组合*)
q = q + dq*dt;
Graphics3D[{robotMoveToQ[q], move3D[frame3D, g[I, L[7], 0]]}], {i, 1, 1000, 1}]
5. 碰撞检测
我们生活的物质世界有一个简单的法则:两个物体不能同时占据同一个空间位置,如果它们试图那么做会有很大的力将它们分开。可是仿真是在虚拟的数字世界中进行的,这个世界可不遵守物质世界那套力的法则,因此仿真还不够真实。为了让机器人仿真更接近实际,我们需要考虑“碰撞检测”(Collision Detection)功能。为了追求效率,工业机器人的运动速度通常比较快,而且抓着较重的负载,它一旦碰到障碍物或者人,结果一般是“物毁人伤”。所以在仿真时提前检测是否有碰撞很有必要。在一些规划算法中,碰撞检测也是很重要的一部分。
值得一提的是,现在一些先进的机器人控制器开始配备简易的碰撞检测功能,如果在机器人工作时有人突然挡住了它,它会自动停止。这是通过检测机械臂关节处电机的电流大小实现的。当机械臂碰到人时,它相当于受到了一个阻力,电机要想保持原来的速度运行需要加大电流,灵敏的控制器会感知到电流的波动,这样我们就能通过监视电流来判断机械臂有没有发生碰撞,如果电流超过一定范围就认为机械臂发生碰撞了,需要紧急刹车。可是这种碰撞检测方法只适用于小负载(<5kg)的机械臂。因为对于重型机械臂,即便它也会停下来,可是它的惯性太大需要一段刹车距离,这足以对人造成伤害。
碰撞检测是一个比较有难度的几何问题,目前有很多成熟的算法(AABB、GJK)。我们的关注点在机器人,所以不想在碰撞检测算法上浪费太多时间。为此,我们使用 Mathematica 自带的 RegionDisjoint 函数实现碰撞检测。在帮助文档中,可以了解到 RegionDisjoint 函数用于判断多个几何体是否相交,如果两两之间都不相交则返回 True ,而两个几何体出现了相交,就表示它们发生了碰撞(太好了,这简直是为碰撞检测量身定做的函数)。
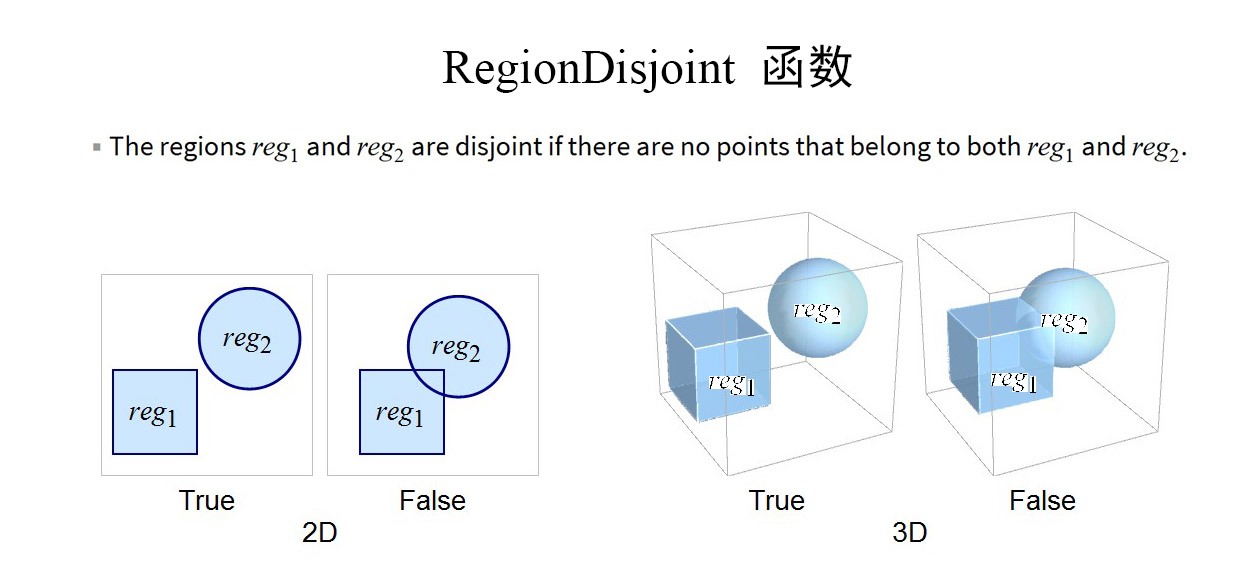
RegionDisjoint 函数可以用于二维几何图形,也可以用于三维几何体,甚至可以用于非凸的几何图形或几何体,如下面的例子所示。例子代码如下,其中使用了Locator控件。

Manipulate[
pts = {{0.95, 0.31}, {0.36, -0.12}, {0.59, -0.81}, {0., -0.38}, {-0.59, -0.81}, {-0.36, -0.12}, {-0.95, 0.31}, {-0.22, 0.31}, {0., 1.}, {0.22, 0.31}, {0.95, 0.31}};
obstacle1 = Disk[pt1, 1];
obstacle2 = Polygon[pt2 + # & /@ pts];
color = If[RegionDisjoint[obstacle1, obstacle2], Green, Red];
Graphics[{EdgeForm[Black], color, obstacle1, obstacle2}, PlotRange -> 3], {{pt1, {-1, -1}}, Locator}, {{pt2, {1, 1}}, Locator}] 不过有了 RegionDisjoint 函数并不意味着一帆风顺。“碰撞检测”是出了名的吞噬者,它会霸占 CPU 大量的计算资源。如果不把它伺候好,你的计算机再先进都会卡死。我们一般希望碰撞检测越快越好,可是精度和速度是一对矛盾,追求速度只能牺牲一定的精度。机械臂的真实外形往往都是不规则的复杂几何体,这使得精确的碰撞检测很浪费时间。多数情况下,我们没有必要达到非常逼真的检测效果。如果不追求很高的精度,碰撞检测应该保守一些。也就是说,在实际没发生碰撞时允许误报,但在发生碰撞时不能漏报——宁可错杀一千,不可放过一个。碰撞检测的计算量与模型的复杂程度有关。我们导入的机器人模型虽然已经经过了“瘦身”,但对于RegionDisjoint函数来说还是有些复杂。为此,我们需要进一步缩减简化。为了保守一点,我们采用比真实机械臂连杆稍大些的模型,比如连杆的凸包(Convex Hull)。虽然 Meshlab 软件可以制作凸包,但是我发现效果不太好。好在 Mathematica 自带的 ConvexHullMesh 函数可以计算任意几何体的凸包。我采用的方法是先用 ConvexHullMesh 分别计算各连杆的凸包,再导出凸包用 Meshlab 进一步简化,最后再导入回 Mathematica 中。计算连杆凸包及导出所需的代码如下。(注意:由于连杆数据已经是变换后的了,简化后的连杆导入后不需要旋转等变换)
robotPartsCH = Table[
pts = robotParts[[i, 1]];
poly = robotParts[[i, 2, 2, 1]];
R = ConvexHullMesh[pts];
pts = MeshCoordinates[R];
poly = MeshCells[R, 2];
R = MeshRegion[pts, poly];
Export["D:\\MOTOMANCH\\" <> partsName[[i]], R];
GraphicsComplex[pts, poly], {i, 7}];
Graphics3D[robotPartsCH]我们检验一下机械臂和外部障碍物的碰撞检测,至于机械臂连杆之间的碰撞我们暂时不考虑。代码如下,效果如下图所示。
Manipulate[
Robs = cuboid[{1.3, 0, 0.5}, {0.5, 0.5, 1.0}]; (*障碍物,一个长方体*)
gs = robotPartsKinematics[{IdentityMatrix[4], {q1, q2, q3, q4, q5, q6}}];
Rparts = Table[MeshRegion[TransPt[gs[[i]]] /@ robotParts[[i, 1]], robotParts[[i, 2, 2]]], {i, 7}];
collisionQ = And @@ (RegionDisjoint[Robs, #] & /@ Rparts);
color = If[collisionQ, Black, Red];
text = If[collisionQ, "哈哈,没事", "啊...碰撞了!"];
Graphics3D[{Gray, Robs, Text[Style[text, FontSize -> 20, FontFamily -> "黑体", FontColor -> color], {-0.5, 1, 1.5}], {MapThread[move3D, {robotPartsColored, gs}]}}, plotOptions], Grid[{{Control[{{q1, 0}, -Pi, Pi, 0.1}],Control[{{q2, 0}, -Pi, Pi, 0.1}]}, {Control[{{q3, 0}, -Pi, Pi, 0.1}], Control[{{q4, 0}, -Pi, Pi, 0.1}]}, {Control[{{q5, 0}, -Pi, Pi, 0.1}], Control[{{q6, 0}, -Pi, Pi, 0.1}]}}], TrackedSymbols :> True]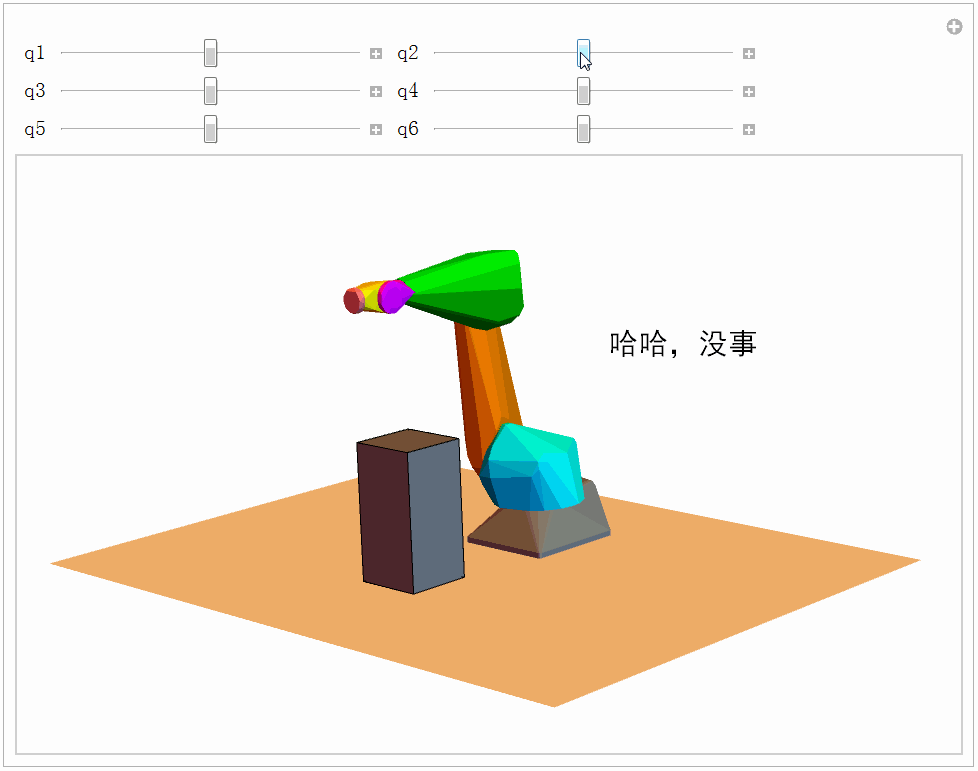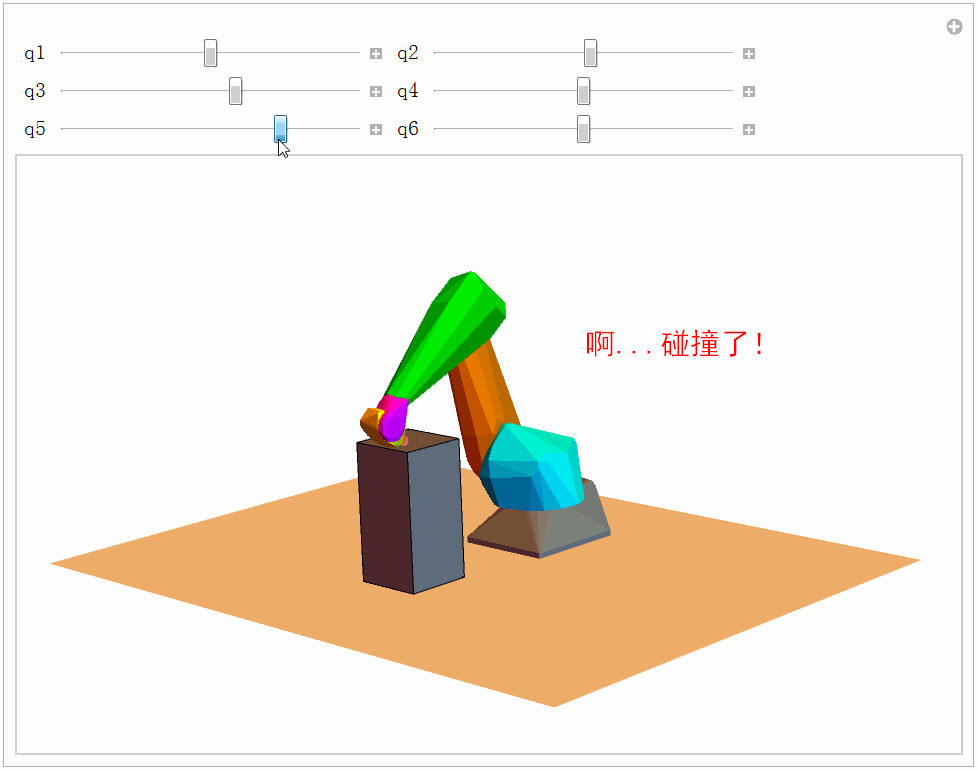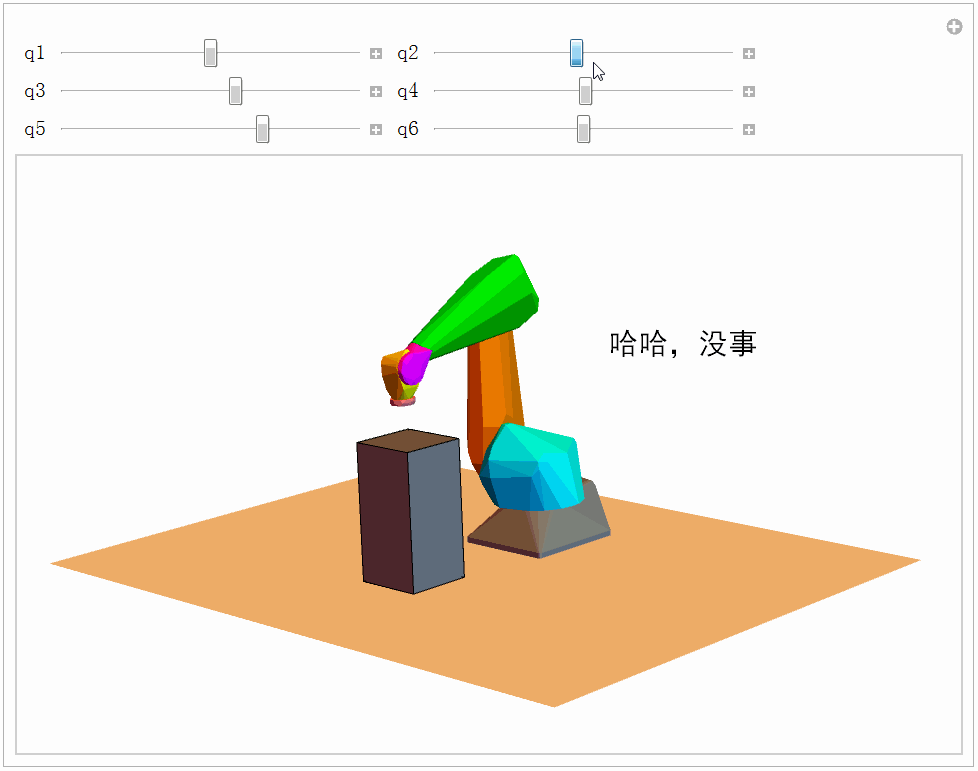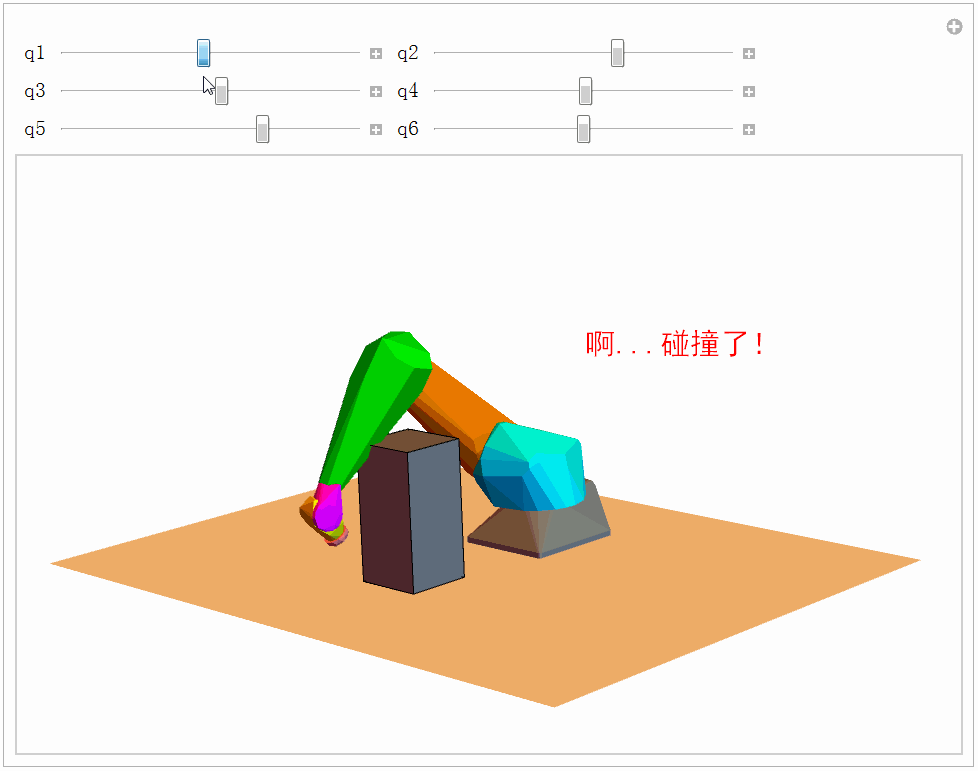
其中,TransPt[g][pt3D] 函数的功能是用齐次变换矩阵 g 对三维向量(点) pt3D 做变换,定义如下:
TransPt[g_][pt3D_]:=Module[{homogeneousPt},
homogeneousPt=Join[pt3D,{1.0}];
homogeneousPt=g.homogeneousPt;
homogeneousPt[[1;;3]] ]6. 轨迹规划
轨迹规划的目的是得到机器人的参考运动轨迹,然后机器人再跟踪这条轨迹完成最终的动作。轨迹规划是机器人研究领域非常重要的一部分。机器人要干活就离不开运动,可是该如何运动呢?像系鞋带、叠被子、翻字典这样的动作对人类来说轻而易举,可要是让机器人来实现就非常困难。工业机器人既没有会思考的大脑,也缺少观察世界的眼睛(又瞎又傻),要让它们完全自主运动真是太难为它们了。它们所有的运动都是人教给它的。你可以把机器人想象成木偶,木偶看起来像是有灵魂的生物,但实际上它的运动都是人灌输的,木偶只会死板地按照人的控制运动,自己没有任何主动性,只是行尸走肉罢了。实际工厂中,是由工程师操作着控制面板,一点点调节机械臂的各个关节角度,让它到达某个位置。控制程序会记录机械臂的角度变化,只要工程师示教一次,机械臂就能精确而忠实地重复无数次。不过这种不得已而为之的方法实在是太笨了,如果有一种方法能够自动根据任务生成机器人的参考轨迹多好,下面我们将介绍一种常用的轨迹规划方法。
6.1 路径、轨迹——傻傻分不清楚
“轨迹”是什么?要理解轨迹可离不开路径。路径(Path)和轨迹(Trajectory)是两个相似的概念,它们的区别在于:
● 路径只是一堆连续空间坐标,它不随时间变化。例如下图左侧的三维曲线就是一段路径。
● 轨迹是运动的坐标,它是时间的函数,一个时刻对应一个空间坐标点。轨迹包含的信息更多,我们可以对它微分得到速度、加速度等信息,而路径是没有这些的。下图右侧展示了两条轨迹,它们虽然经过相同的路径,但却具有不同的速度——黑色轨迹开始运动较快,随后被红色反超,最后二者又同时到达终点,所以它们是两条轨迹(而不是一条)。
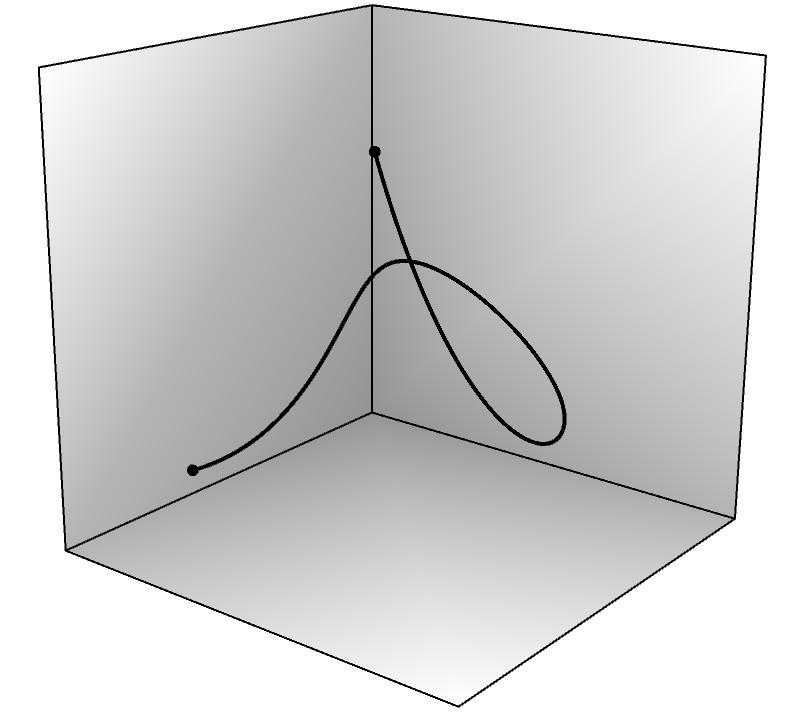
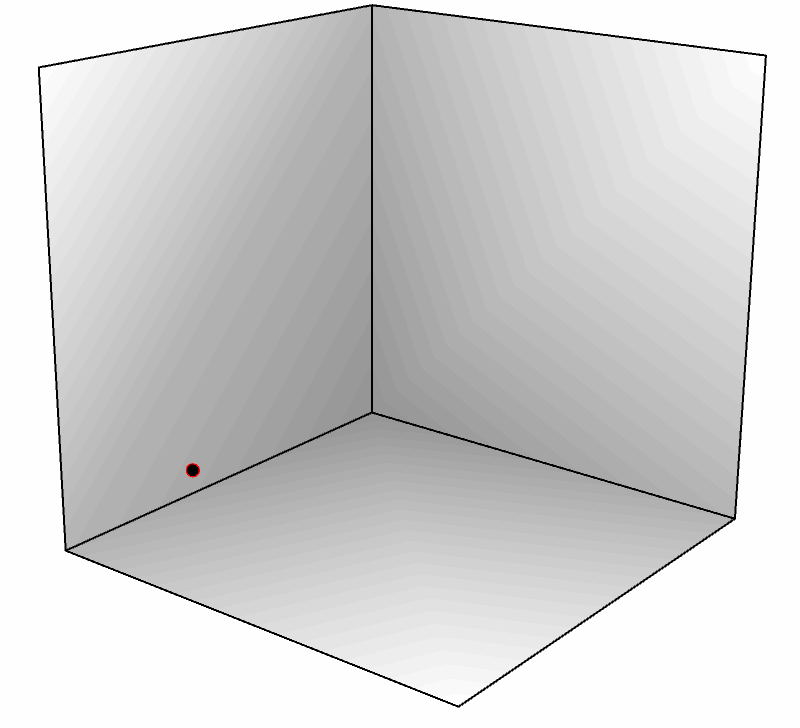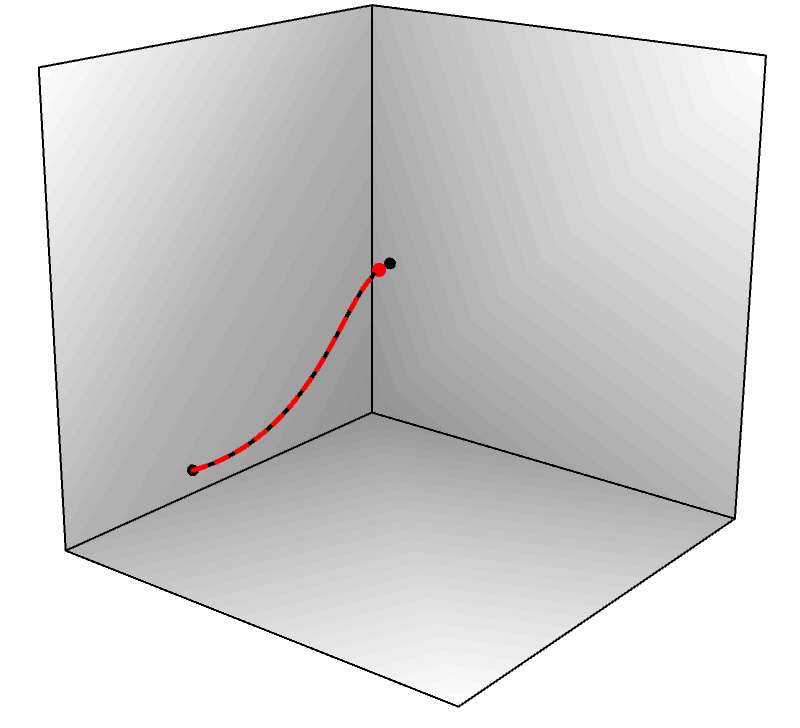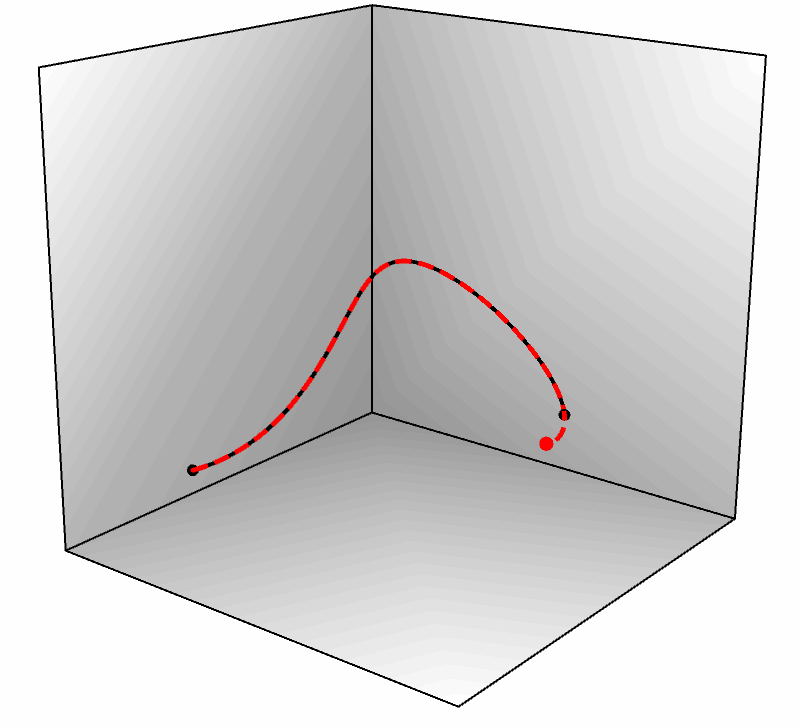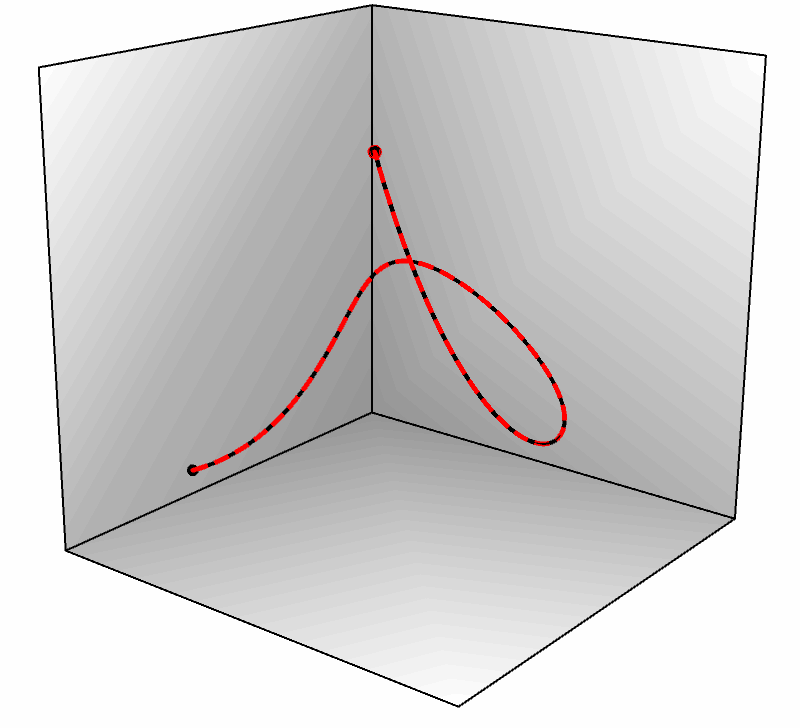
如果我们画出红色和黑色轨迹的 $x,y,z$ 坐标分量,就会看到它们从同一位置出发,又在另一个位置碰头,却经历了不同的过程,如下图所示(注意红黑两组曲线的开始和结尾)。
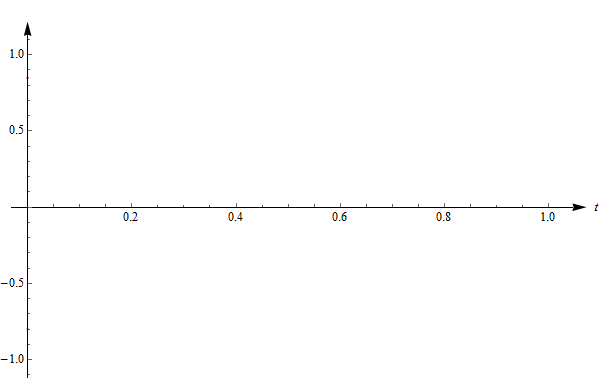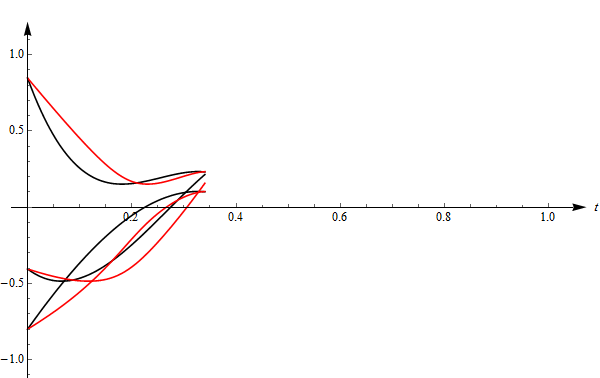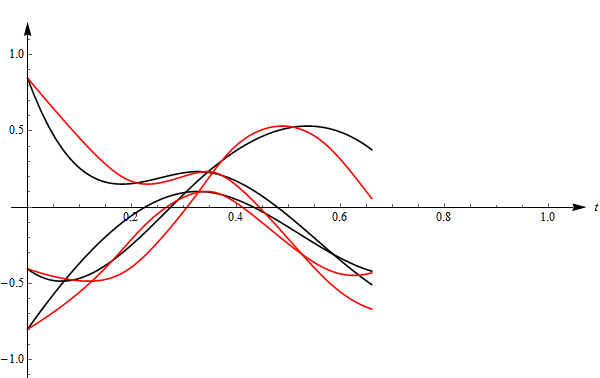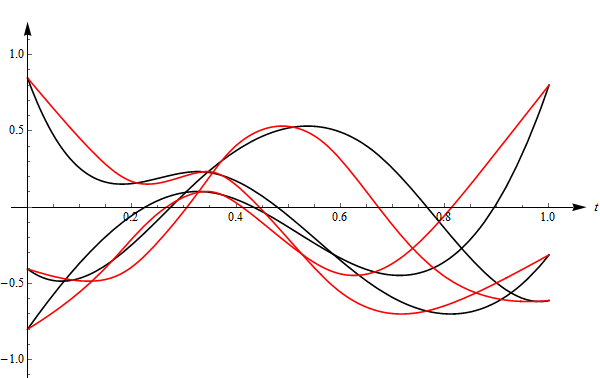
制作上面的轨迹需要以下几个步骤:
1. 首先随机生成一些三维空间中的点。
pts = RandomReal[{-1,1},{6,3}]; (*6个三维坐标点*) 2. 然后利用 BSplineFunction 函数对点插值。
bfun = BSplineFunction[pts]; 所得到的 bfun 是一个( B 样条)插值函数,它的自变量的取值范围是 $0∼1$,你可以用 ParametricPlot3D[bfun[t], {t, 0, 1}] 画出这条曲线。
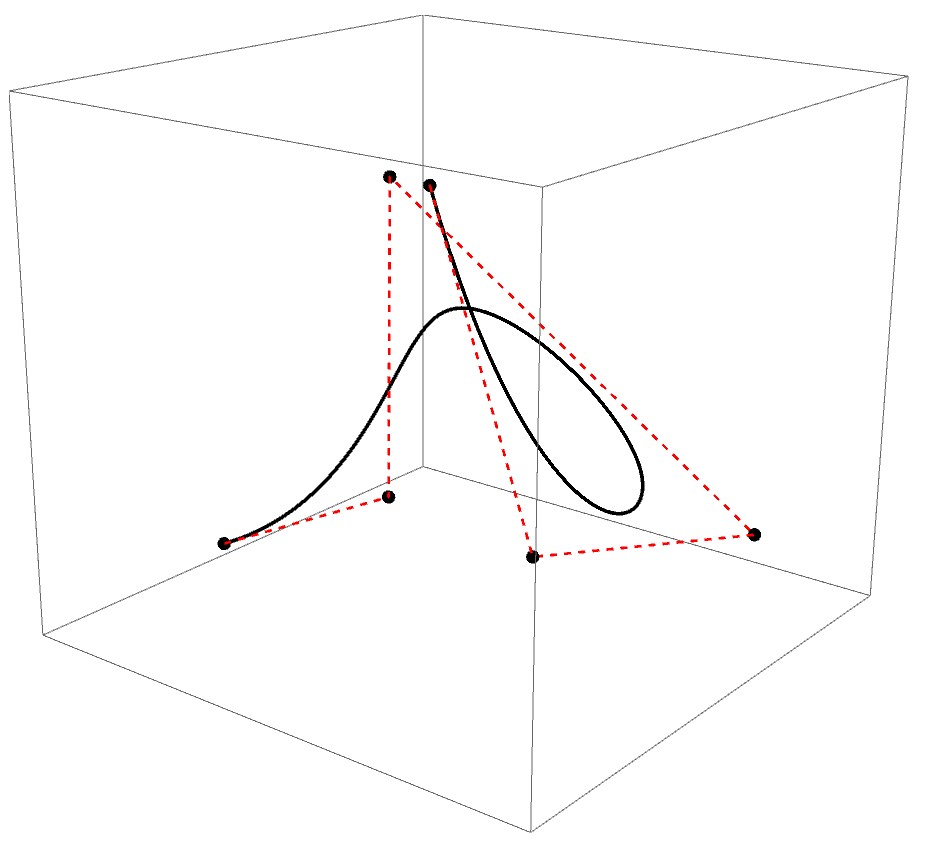
3. 二次插值。我们虽然得到了插值函数,但它是一个向量值函数,难以进一步处理(比如求积分、微分)。所以,我们需要在 bfun 函数的基础上再处理。首先得到 bfun 函数图像上若干离散点(按照0.001的间隔取):
bfpts = bfun /@ Range[0, 1, 0.001]; 然后分别对xyz坐标分量进行单独插值(这里我同样将自变量的取值范围设定在0∼1之间):
nb = Length[bfpts];
ifunx=Interpolation[Transpose[{Range[0,1,1/(nb-1)],bfpts[[;;,1]]}]];
ifuny=Interpolation[Transpose[{Range[0,1,1/(nb-1)],bfpts[[;;,2]]}]];
ifunz=Interpolation[Transpose[{Range[0,1,1/(nb-1)],bfpts[[;;,3]]}]];并定义一个新的插值函数为各分量的合成。这样我们就人为生成了一段轨迹(或者说,是一个向量值函数)。
ifun[t_] := {ifunx[t], ifuny[t], ifunz[t]} 我们能对这段轨迹做什么呢?
● 可以计算它的弧长,代码如下:
ArcLength[ifun[t], {t, 0, 1}]● 既然可以计算弧长,就能用弧长对这条曲线重新参数化(我以前在学高等数学时,一直想不通怎么用弧长对一个曲线参数化,现在通过编程实践就很容易理解了):
arcLs = Table[ArcLength[Line[bfpts[[1 ;; i]]]], {i, Length[bfpts]}]/ArcLength[Line[bfpts]];
ifunArcx = Interpolation[Transpose[{arcLs, bfpts[[;; , 1]]}]];
ifunArcy = Interpolation[Transpose[{arcLs, bfpts[[;; , 2]]}]];
ifunArcz = Interpolation[Transpose[{arcLs, bfpts[[;; , 3]]}]];
ifunArc[t_]:= {ifunArcx[t], ifunArcy[t], ifunArcz[t]}我们可以观察两种参数化的轨迹的图像:
Animate[ParametricPlot3D[{ifun[t], ifunArc[t]}, {t, 0, end}, PlotStyle -> {{Thick, Black}, {Thin, Dashed, Red}}, PlotRange -> 1], {end, 0.01, 1, 0.01}] 我们说路径携带的信息比轨迹少,那么从路径中能提取出什么有价值的信息呢?
路径只包含几何信息:对于一个三维空间中的光滑路径,我们能计算这条路径上每一点处的切线和法线,它们刚好能唯一地确定一个右手直角坐标系(这个坐标系又被称为 Frenet 标架),如下图所示。对应的代码如下。大家都知道,平面上的曲线可以用曲率描述它的弯曲程度,可是要描述三维空间曲线的弯曲程度还需要一个量,叫挠率,它是描述扭曲程度的。如果把Frenet 标架想象成过山车,你坐在上面就能更直观地感受曲率和挠率的含义。
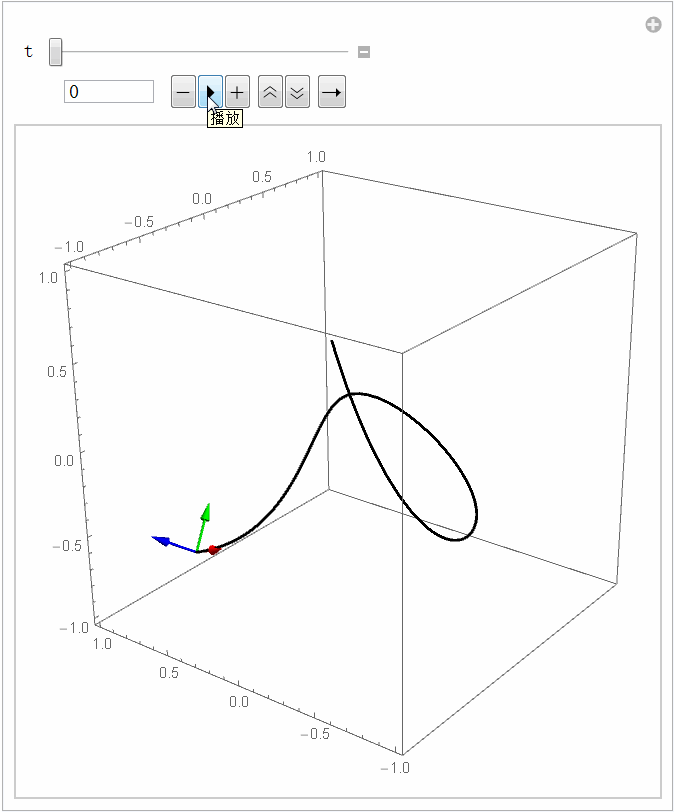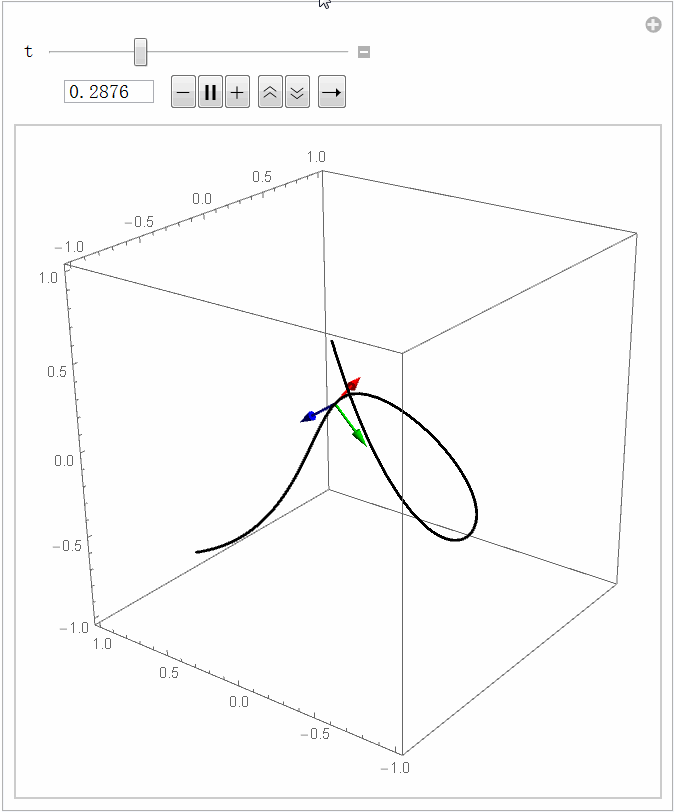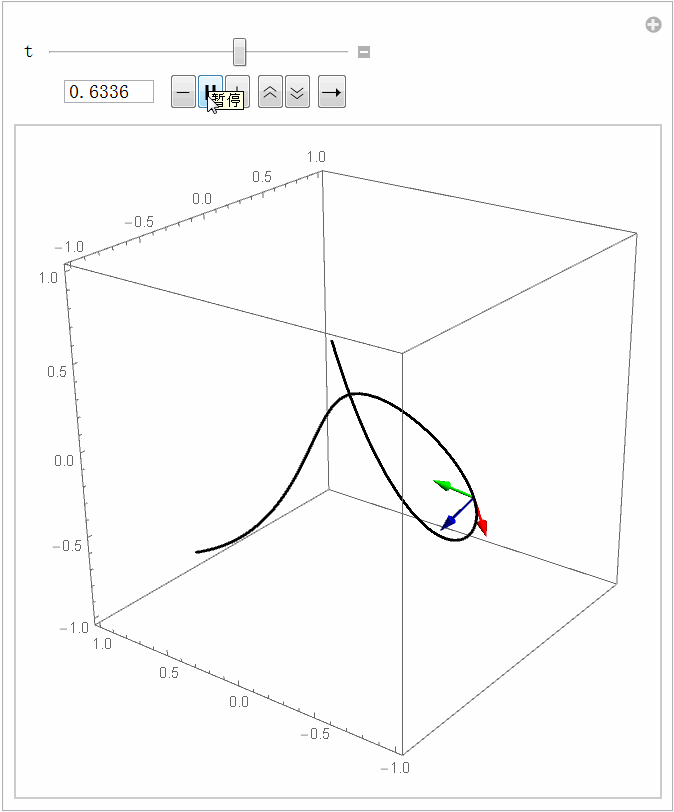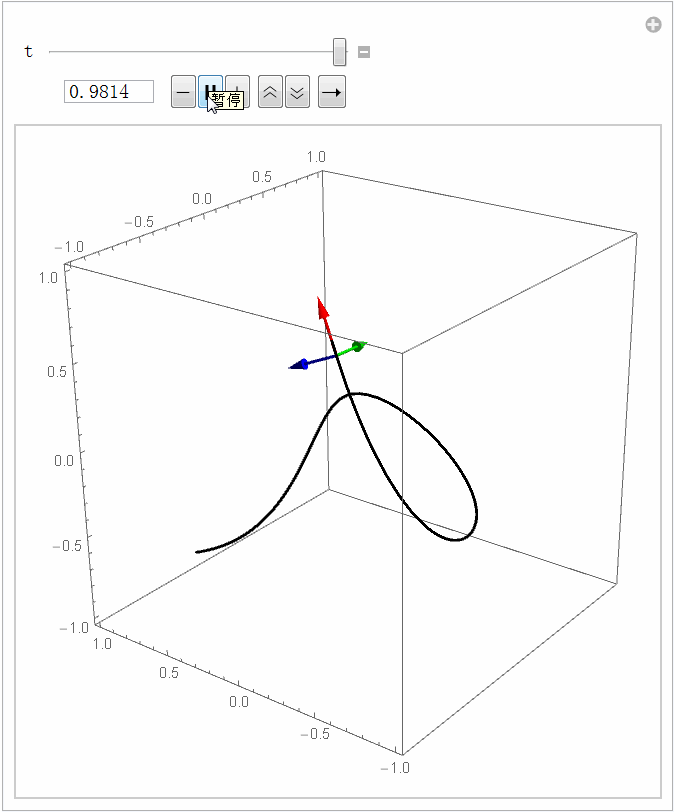
basis = Last@FrenetSerretSystem[ifun[x],x];
p1 = ParametricPlot3D[ifun[t],{t,0,1},PlotRange->1];
Manipulate[pt = ifun[t];
tangent = Arrow[Tube[{pt,pt+(basis[[1]]/.x->t)/3}]];
normal = Arrow[Tube[{pt,pt+(basis[[2]]/.x->t)/3}]];
binormal= Arrow[Tube[{pt,pt+(basis[[3]]/.x->t)/3}]];
p2 = Graphics3D[{Arrowheads[0.03],Red,tangent,Green,normal,Blue,binormal}];
Show[p1,p2],{t,0,1,Appearance->{"Open"}}]还可以制作任意你想要的路径,例如制作一条“文字轮廓”路径的代码如下:
text = Text[Style["欢", Bold]];
tg = DiscretizeGraphics[text, _Text, MaxCellMeasure -> 0.005]; (*数值越小,点越密*)
pts = MeshCoordinates[tg];
pts = pts[[Last[FindShortestTour[pts]]]]; 然后将其显示出来。这里得到的是二维点的坐标,要想让我们的机械臂跟踪,需要将其转换为三维坐标,这很简单,你可以直接用替换命令:pts3D = pts /. {x_, y_} -> {x, y, 1.5}。
Manipulate[Graphics[{Line[pts[[1 ;; i]]]}, PlotRange -> 10, GridLines -> Automatic], {i, 1, Length[pts], 1}]
6.2 轨迹规划方法
爱丽丝:你能告诉我要走哪条路吗?
柴郡猫:那得看你要去哪里。
爱丽丝:我也不太知道要去哪里。
柴郡猫:那走哪条路都没有关系了。
———《爱丽丝梦游仙境》
“轨迹规划”中的“规划”到底是什么意思呢?规划的英文是 plan,也翻译为“计划、策划”。你肯定知道“计划”是什么意思。对于人来说,计划就是在做事之前先想想应该怎么做才好,比如沿着什么途径、按照哪几个步骤。谈到计划,首先你得有一个要到达或者要实现的目标,没有目标谈不上计划(当然一般还得有一个出发点,但这不是必需的)。假如我放假想出去玩,在制定了详细的开车路线后我连要去哪都不知道,那我是不是神经病呢。正常人都是先决定去哪,然后才选择交通线路。上面爱丽丝和柴郡猫的对话就充满了哲理,你要是没有目标,那精心选择路径又有什么意义呢。
此外,计划还有个评价的标准——怎么样才算“好”呢?如果没有标准,那我们还计划个什么劲儿啊(反正没有好坏之分)?所以规划有两个基本要素——目标和评价标准。把目标和评价标准推广到机器人的轨迹规划领域,问题就是:机器人怎么(运动)才能到达一个目标位置,而且不仅仅是到达目标这么简单,我们还想以最好的方式(比如时间最短、消耗的能量最少)到达,这就是轨迹规划的任务。“轨迹规划”的叫法挺多,有叫“轨迹生成”的,有叫“轨迹搜索”的,有叫“运动规划”的,但不管怎么叫其实大概都是一个意思。
对于机械臂来说,轨迹规划方法可以根据有没有障碍物来划分。如果没有障碍物,那就简单些了,我们可以直接规划轨迹。你看到的工业机器人轨迹规划一般都属于这种,是不是听上去高大上但其实很傻。如果有障碍物则一般先规划路径(因为路径包含信息更少,相对更简单),然后对路径设置速度得到轨迹(因为主要的工作都在规划路径,因此也可称其为“路径规划”)。有趣的是,对于无人驾驶汽车来说,它的轨迹规划方法也是先规划路径,再在路径上规划速度。
路径规划都有哪些方法呢?比较流行的有:图搜索、势场法、RRT 等等。下面我们来实现 RRT 方法。
RRT(快速探索随机树) 是一种通用的方法,不管什么机器人类型、不管自由度是多少、不管约束有多复杂都能用。而且它的原理很简单,这是它在机器人领域流行的主要原因之一。不过它的缺点也很明显,它得到的路径一般质量都不是很好,例如可能包含棱角,不够光滑,通常也远离最优路径。


RRT 能在众多的规划方法中脱颖而出,它到底厉害在哪里呢?
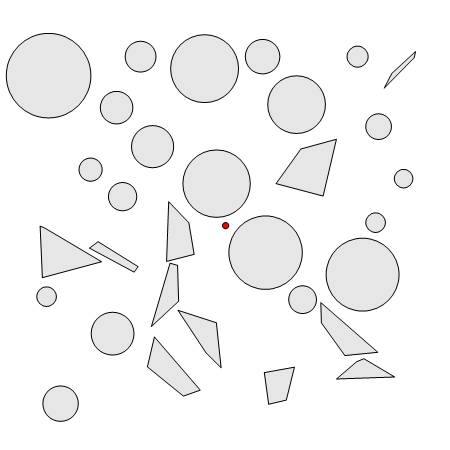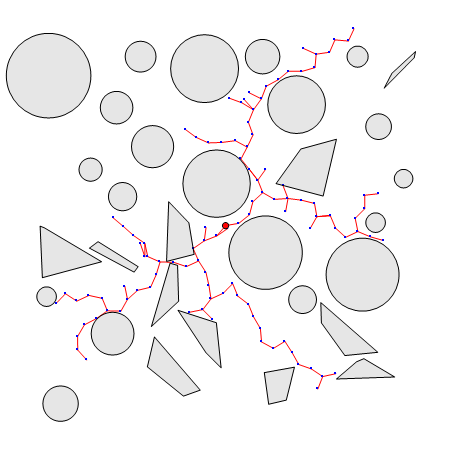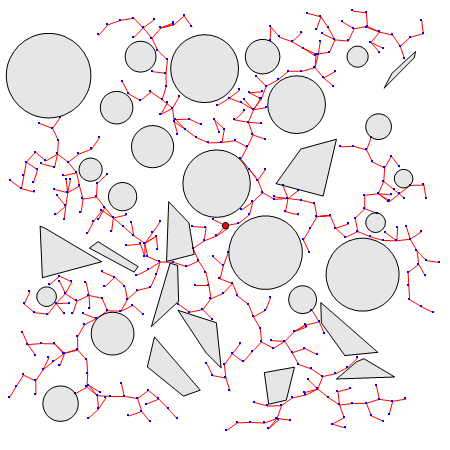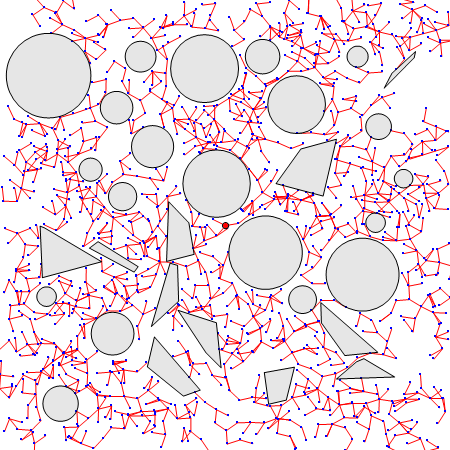
天下武功唯快不破,“快”是 RRT 的一大优点。RRT 的思想是快速扩张一群像树一样的路径以探索(填充)空间的大部分区域,伺机找到可行的路径。之所以选择“树”是因为它能够探索空间。我们知道,阳光几乎是树木唯一的能量来源。为了最大程度地利用阳光,树木要用尽量少的树枝占据尽量多的空间。当然了,能探索空间的不一定非得是树,比如Peano曲线也可以做到,而且要多密有多密,如上图左所示的例子。虽然像Peano曲线这样的单条连续曲线也能探索空间,但是它太“确定”了。在搜索轨迹的时候我们可不知道出路应该在哪里,如果不在“确定”的搜索方向上,我们怎么找也找不到(找到的概率是0)。这时“随机”的好处就体现出来了,虽然不知道出路在哪里,但是通过随机的反复试探还是能碰对的,而且碰对的概率随着试探次数的增多越来越大,就像买彩票一样,买的数量越多中奖的概率越大(RRT名字中“随机”的意思)。可是随机试探也讲究策略,如果我们从树中随机取一个点,然后向着随机的方向生长,那么结果是什么样的呢?见上图右。可以看到,同样是随机树,但是这棵树并没很好地探索空间,它一直在起点(红点)附近打转。这可不好,我们希望树尽量经济地、均匀地探索空间,不要过度探索一个地方,更不能漏掉大部分地方。这样的一棵树怎么构造呢?
RRT 的基本步骤是:
1. 将起点作为一颗种子,从它开始生长枝丫;
2. 在机器人的“构型”空间中,生成一个随机点A;
3. 在树上找到距离A最近的那个点,记为B吧;
4. B朝着A的方向生长,如果没有碰到障碍物就把生长后的树枝和端点添加到树上,返回 2;
随机点一般是均匀分布的,所以没有障碍物时树会近似均匀地向各个方向生长,这样可以快速探索空间(RRT名字中“快速探索”的意思)。当然如果你事先掌握了最有可能发现路径的区域信息,可以集中兵力重点探索这个区域,这时就不宜用均匀分布了。
RRT 的一个弱点是难以在有狭窄通道的环境找到路径。因为狭窄通道面积小,被碰到的概率低,找到路径需要的时间要看运气了。下图展示的例子是 RRT 应对一个人为制作的很短的狭窄通道,有时RRT很快就找到了出路,有时则一直被困在障碍物里面。对应的代码如下(这段代码只用于演示 RRT 的原理,不是正式代码,但它有助于理解正式代码的运算过程):
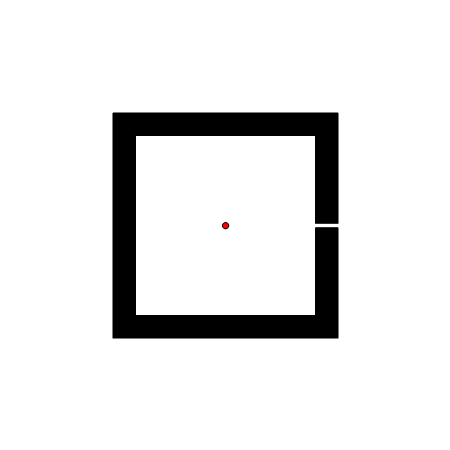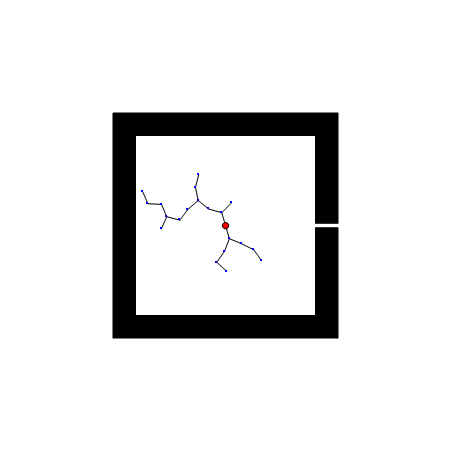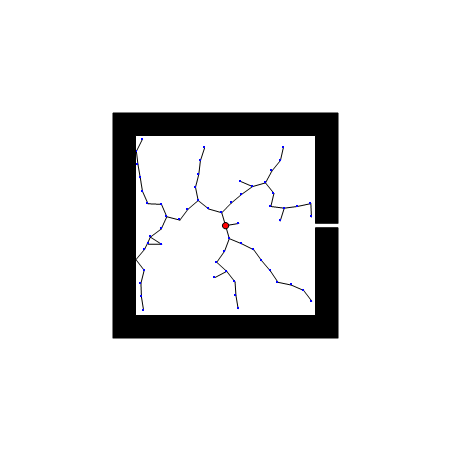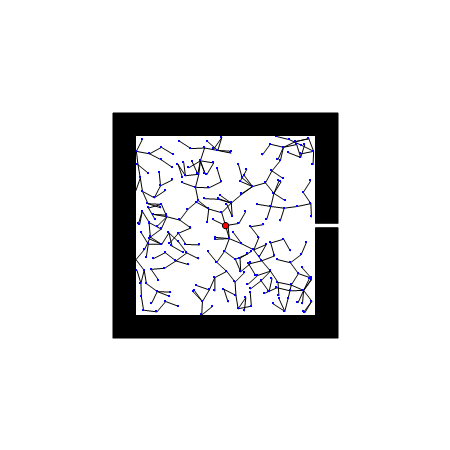
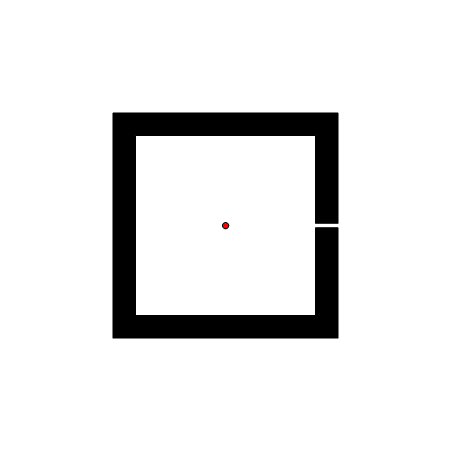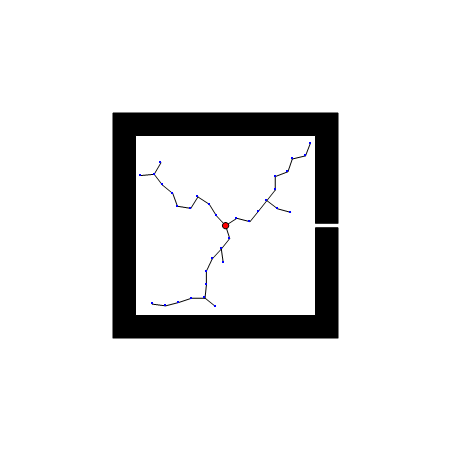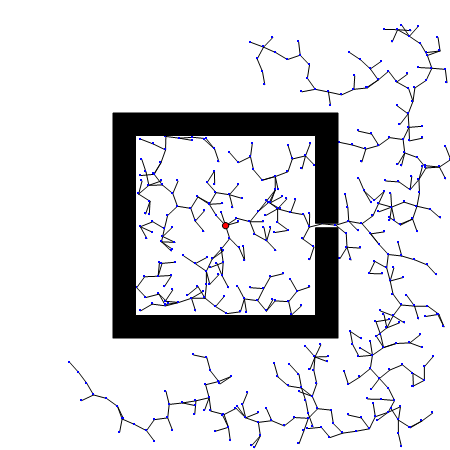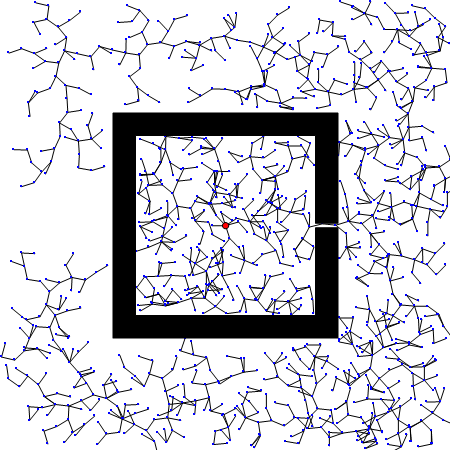
(*RRT示例:此段程序不依赖任何自定义函数,可独立运行。这是我能想到的最短的RRT演示代码了*)
step = 3; maxIters = 2000; start = {50, 50}; range = {0, 100};
pts = {start}; lines = {{start, start}};
obstaclePts = {{20, 1}, {25, 1}, {25, 25}, {-25, 25}, {-25, -25}, {25, -25}, {25, -1}, {20, -1}, {20, -20}, {-20, -20}, {-20, 20}, {20, 20}} + 50;
Do[randomPt = RandomReal[range, 2];
{nearestPt} = Nearest[pts, randomPt, 1];
grownPt = nearestPt + step*Normalize[randomPt - nearestPt];
If[!Graphics`Mesh`IntersectQ[{Line[{nearestPt, grownPt}], Polygon[obstaclePts]}],
AppendTo[lines, {nearestPt, grownPt}];
AppendTo[pts, grownPt]], {maxIters}];
Animate[Graphics[{Polygon[obstaclePts], Line[lines[[1 ;; i]]], Blue, PointSize[0.004], Point[pts[[1 ;; i]]], Red, Disk[start, 0.7]}, PlotRange -> {range, range}], {i, 1, Length[pts] - 1, 1}] RRT探索空间的能力还是不错的,例如下图左所示的例子,障碍物多而且杂乱(借助 Mathematica 本身具有的强大函数库,实现这个例子所需的所有代码应该不会超过30行)。还有没有环境能难住RRT呢?下图右所示的迷宫对RRT就是个挑战。这个时候空间被分割得非常严重,RRT显得有些力不从心了,可见随机策略不是什么时候都有效的。
“随机”使得RRT有很强的探索能力。但是成也萧何败也萧何,“随机”也导致 RRT 很盲目,像个无头苍蝇一样到处乱撞。如果机器人对环境一无所知,那么采用随机的策略可以接受。可实际情况是,机器人对于它的工作环境多多少少是知道一些的(即使不是完全知道)。我的博客一直强调信息对于机器人的重要性。这些已知的信息就可以用来改进算法。一个改进的办法就是给它一双“慧眼”:在势场法中,势函数携带了障碍物和目标的信息,如果能把这个信息告诉 RRT,让它在探索空间时有倾向地沿着势场的方向前进会更好。这样,RRT 出色的探索能力刚好可以弥补势场法容易陷入局部极小值的缺点。

将RRT方法用在机械臂上的效果如下图所示(绿色表示目标状态)。我设置了4个障碍物(其中一个是大地),这对机械臂是个小小的挑战。由于我们生活在三维空间,没办法看到六维关节空间,所以我把六维关节空间拆成了两个三维空间,分别对应前三个关节和后三个关节(严格来说,六维转动关节空间不是一个欧式空间,它是个流形,不过这里我们不必纠结这个差别):
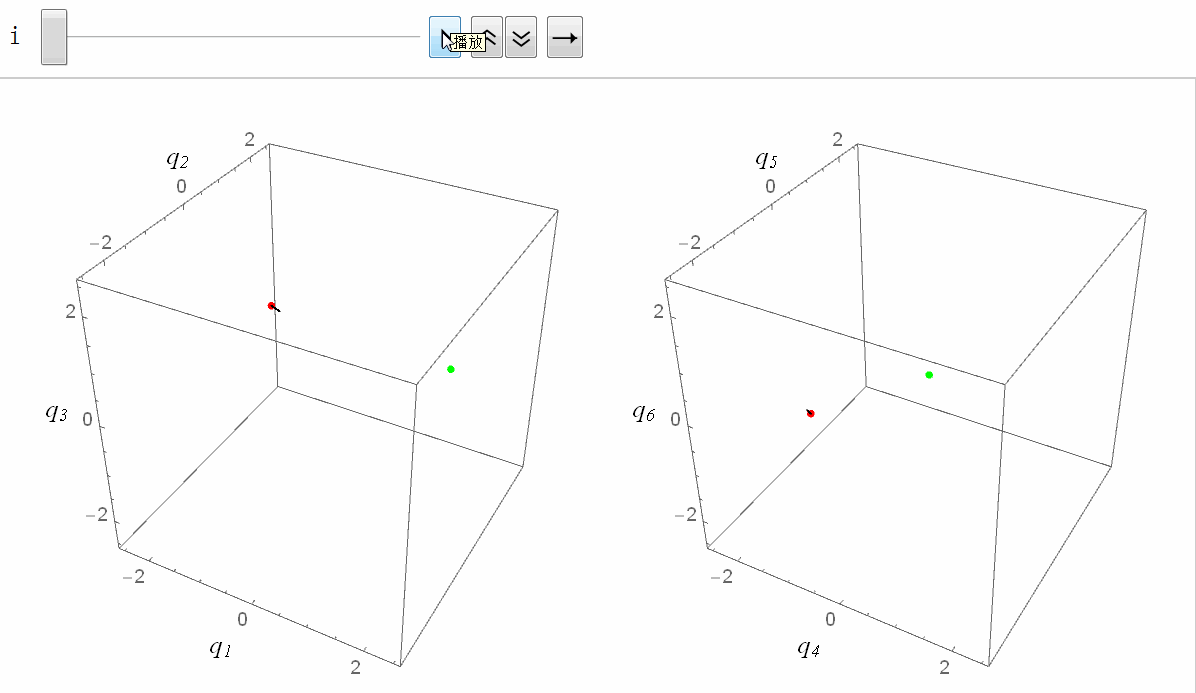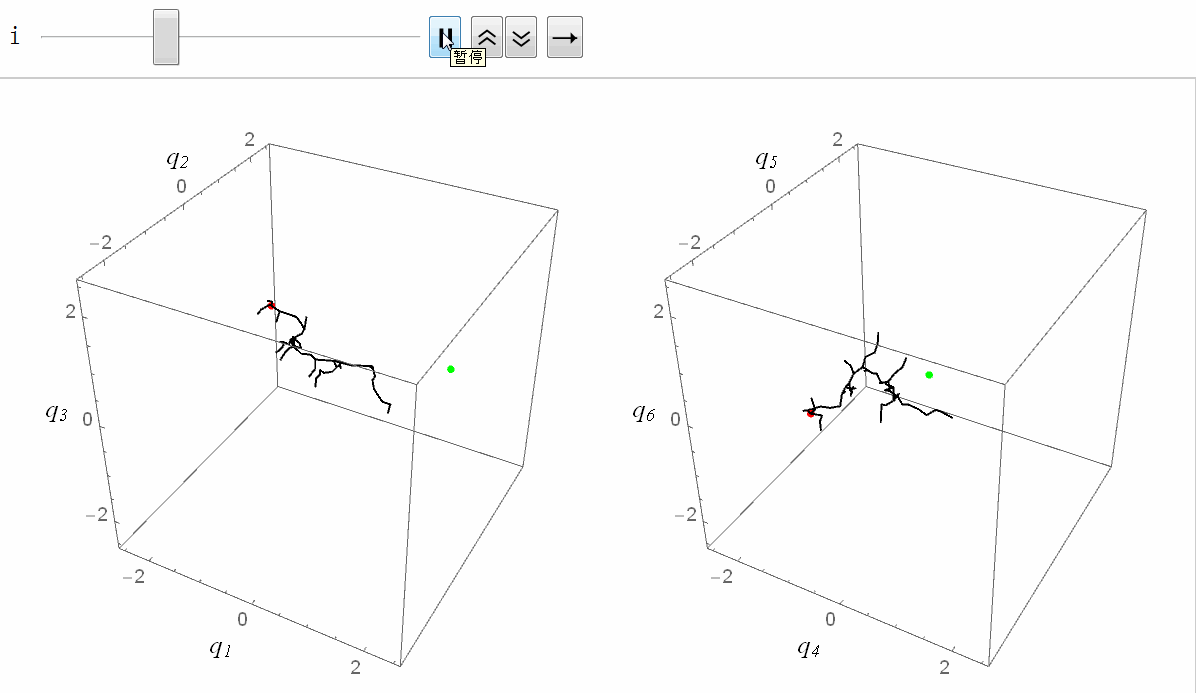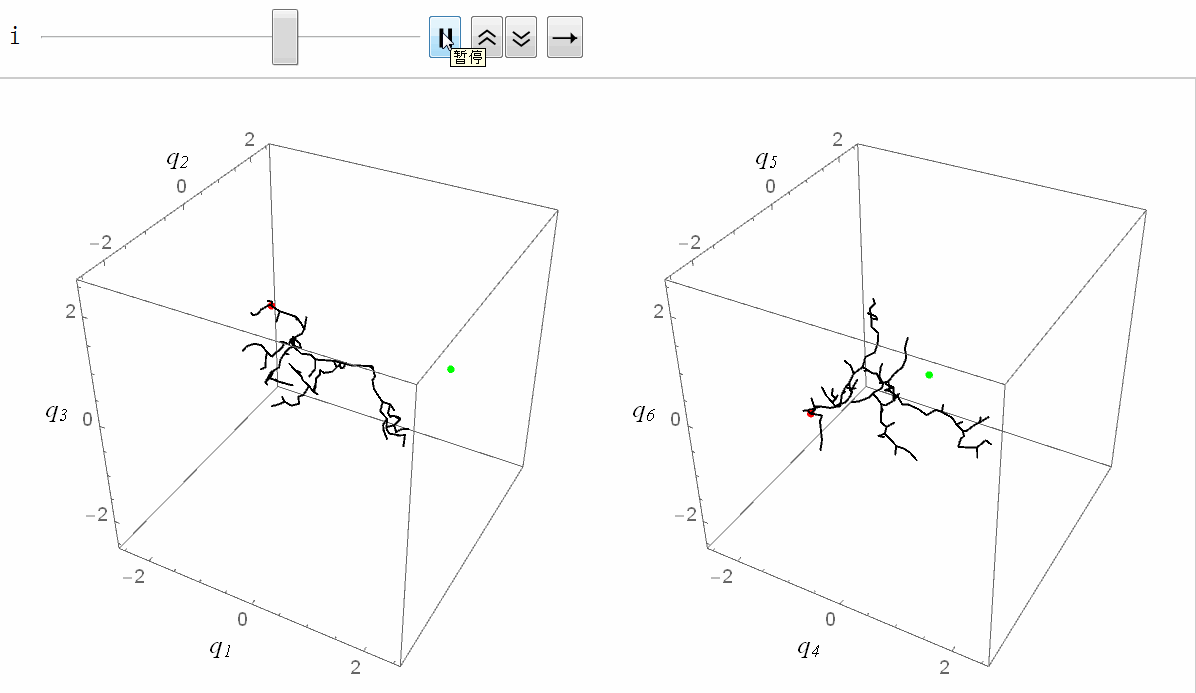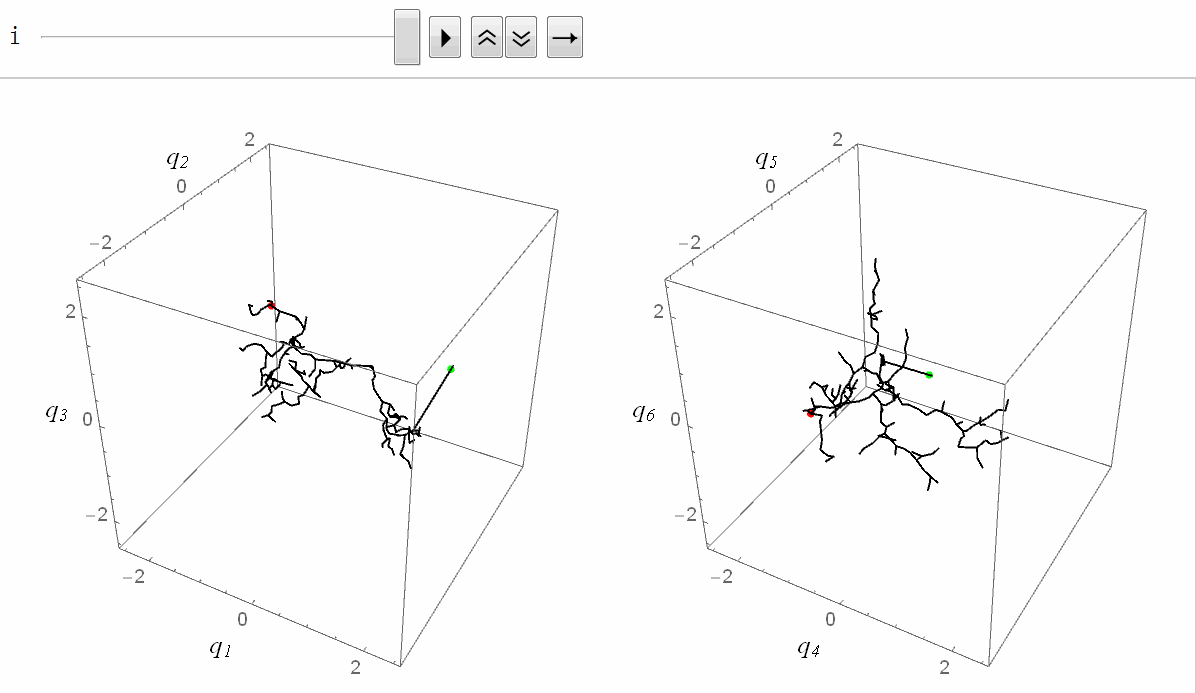
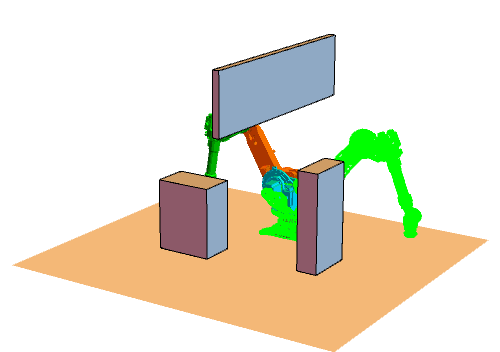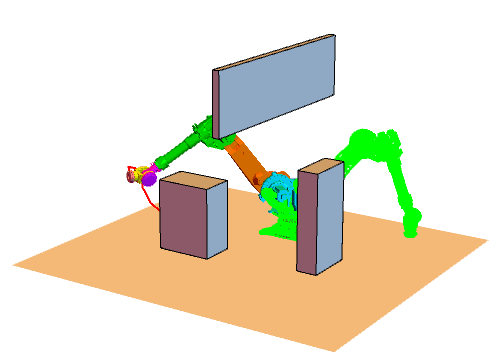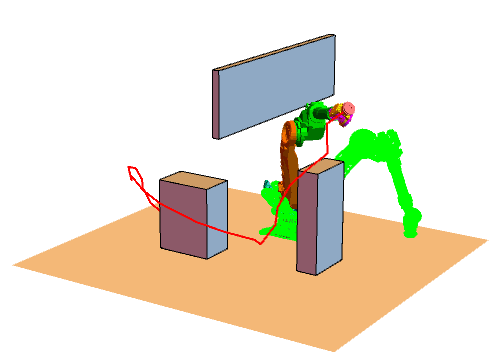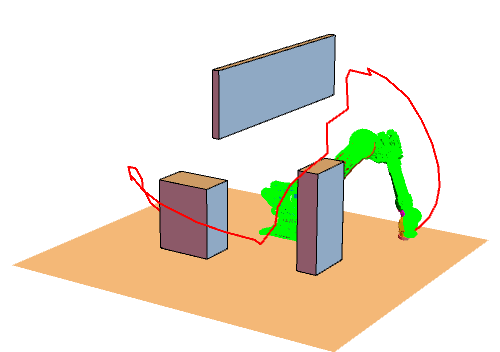
正式 RRT 的主程序代码如下。我将 RRT 树定义为由节点列表 nodes 和树枝列表 edges 组成,即 RRTtree = {nodes, edges}。其中节点列表 nodes 存储树中所有节点(每个节点都是一个 6 维向量,表示机械臂的关节值),树枝列表 edges 中存储所有树枝,树枝定义为两个节点的代号(节点的代号定义为节点被添加到树中的顺序。例如,添加新节点时树中已经有4个节点了,那么新节点的代号就是 5)。
obsCenters = {{0,0,-0.15},{1.4,-0.8,0.5},{1,1,0.7},{0.5,0,2.3}};
obsDims = {{8,8,0.2},{0.5,0.8,1.0},{0.7,0.3,1.4},{3,0.1,0.9}};
Robs = MapThread[cuboid, {obsCenters, obsDims}]; (*定义4个长方体障碍物*)
step = 0.2; (*树枝每次生长的长度,这里简单设置为固定值*)
q0 = {-1.54, 0.76, 0.66, -1.14, -1.44, 0}; (*起点*)
qt = {1.76, 0.76, 0.46, 0, 0.36, 0}; (*目标点*)
nodes = {q0}; (*以起点q0作为种子*)
edges = {}; (*树枝初始为空*)
RRTtree = {nodes, edges}; (*树的初始化由节点和树枝组成,它是全局变量*)
maxIters = 2000; (*最大迭代步数*)
jointLims = {{-Pi, Pi}, {-Pi/2, Pi/2}, {-Pi, 1.45}, {-Pi, Pi}, {-2, 2}, {-Pi, Pi}}; (*关节极限范围,有些关节值不可取*)
qRandList = RandomPoint[Cuboid[ConstantArray[-Pi, n], ConstantArray[Pi, n]], maxIters, jointLims]; (*一次性生成所有的随机点*)
Do[nodes = RRTtree[[1]];
If[Min[Norm /@ ((-qt+#)&/@nodes)] < 0.01, Print["哈哈,到达目标了!"]; Break[]];
qRand = RandomChoice[{qRandList[[i]], qt}]; (*以50%的概率贪婪地着朝目标生长*)
grow[qRand,step], {maxIters}];构造 RRT 树用到了以下自定义的函数:
1. 首先是碰撞检测函数 collisionDetection,如果机械臂没有碰到障碍物就返回True。为了节省时间,碰撞检测使用的是机械臂各连杆的凸包,在最后显示的时候才使用原始连杆。
collisionDetection[Rparts_, Robs_]:= And @@ Flatten@Table[RegionDisjoint[i, #] & /@ Rparts, {i, Robs}] 2. 碰撞检测函数需要 Region 类型的变量,为此定义 toRegion 函数将几何体变换为 Region 类型,代码如下:
toRegion[q_]:= Module[{gs, Rparts},
gs = robotPartsKinematics[{IdentityMatrix[4], q}];
Rparts = Table[MeshRegion[TransPt[gs[[i]]] /@ robotParts[[i, 1]], robotParts[[i, 2, 2]]], {i, 7}]]3. 向RRT树中添加节点和边的函数:
addNode[node_]:= Module[{}, AppendTo[RRTtree[[1]], node]; Length[RRTtree[[1]]] ]
addEdge[edge_]:= Module[{}, AppendTo[RRTtree[[2]], edge]; Length[RRTtree[[2]]] ]4. 树枝朝着采样点生长(为了简单,只检测一点的碰撞情况):
grow[qRand_,step_:0.2]:= Module[{qNearestIdx, qNearest, growAngles},
{qNearestIdx} = Nearest[nodes -> Automatic, qRand, 1];(*最近节点的代号*)
qNearest = nodes[[qNearestIdx]];
growDirection = Normalize[qRand - qNearest];
qExpand = modToPiPi[qNearest + step * growDirection]; (*生长*)
Rrobot = toRegion[qExpand];
If[collisionDetection[Rrobot, Robs], qNewIdx = addNode[qExpand]; (*添加新节点,返回新节点的代号 qNewIdx *)
addEdge[{qNearestIdx, qNewIdx}]] ]下面的代码可以显示搜索到的(关节空间中的)路径。这条路径质量不高,如果用于机器人的轨迹跟踪还需要经过后期的平滑处理。
edges = RRTtree[[2]];
targetIdx = edges[[-1, 2]];
qPath = backTrack[targetIdx];
Animate[Graphics3D[{Robs, robotMoveToQ[qPath[[i]]]}], {i, 1, Length[qPath], 1}] 其中,backTrack 函数用来从树中抽取出连接起点和目标点的路径:
backTrack[nodeIdx_]:= Module[{searchNodeIdx = nodeIdx, nodes = RRTtree[[1]], edges = RRTtree[[2]], searchNodePos, preNodeIdx, pathIdx = {}, pathCoords},
Do[{searchNodePos} = FirstPosition[edges[[All, 2]], searchNodeIdx];
preNodeIdx = edges[[searchNodePos, 1]];
AppendTo[pathIdx, preNodeIdx];
If[preNodeIdx == 1, Break[], searchNodeIdx = preNodeIdx], {Length[edges]}];
pathIdx = Reverse[pathIdx];
pathCoords = nodes[[pathIdx]] ]7. 动力学仿真
如果在淘宝花2块钱买个知网账号,然后检索以“工业机器人控制”为关键词的学位论文,在粗略地浏览了几十篇论文的目录之后,你就会像我一样总结出一个朴素的规律:
● 硕士论文一般都建立了机器人的运动学模型。
● 博士论文一般都建立了机器人的动力学模型。
既然运动学已经能够帮助机器人动起来了,为什么还需要费那么大劲建立动力学(以至于需要博士出马)?
在前面的运动学一节中,我们能通过改变各个关节角度控制机械臂运动。但是在实际机械臂上,关节需要由电机驱动才能改变角度。那么电机应该输出多大的力才能驱动机械臂运动呢,所需要的电流又是多大呢?只有知道这些我们才能真正实现对机械臂的控制。传统的工业机器人大多采用两层的控制方式,上层控制器直接输出角度信号给底层驱动器,底层驱动器负责控制电机的电流实现上层给出的运动。上层不需要知道机器人的动力学特性也可以,更不用管需要输出多大电流。如果你的机器人不需要太高的运动速度和精度,动力学没什么太大用处(运动学是必需的,动力学不是必需的)。可是如果你的机器人速度很快,动力学效应就很明显了,这时就要考虑动力学,否则上层发出的指令底层驱动器跟踪不上,就会出现很大的误差。要想把抓着很重的负载而且高速运动的六轴机器人控制好非常困难,中国好像还没有人能做到。这也是为什么国产机器人大多应用在精度不高的场合,比如搬运、码垛,而进口机器人霸占高端应用的原因。在高级的机器人控制器中,都有力矩补偿功能(例如汇川、KEBA的控制器)。这个补偿的力矩是怎么来的呢?就是通过动力学方程计算得到的。补偿力矩用作前馈控制信号,将其添加到驱动器上能使机器人更好地跟踪一段轨迹。现在机器人在中国变得火热起来了,动力学也成为一些人吹嘘的噱头了。


##### 汇川控制器(动力学补偿使电流更小) KEBA控制器(动力学使跟踪精度更高)
我们如何得到机器人的动力学模型呢?
宅男牛顿首开先河,在同时代的人还浑浑噩噩的时候初步搞明白了力、速度、惯性都是怎么回事,并用数学对其进行了定量描述,从而建立了物体做平移运动时的动力学方程。从牛顿的身上我们知道,学好数学是有多重要。在那个遍地文盲的蛮荒年代,年轻的牛顿已经偷偷地自学了欧几里得、笛卡尔、帕斯卡、韦达等大师的著作,这为他日后发明微积分打下了基础。牛顿谦虚地自称站在巨人的肩上,事实的确如此。
勤奋的欧拉再接再厉,将牛顿的方程推广到转动的情况。哥俩的工作结合起来刚好可以完整地描述物体的运动,这就是“牛顿-欧拉法”。
博学的拉格朗日发扬光大,又将牛顿和欧拉的工作总结提炼,提出了“拉格朗日法”。拉格朗日真聪明啊,只需要计算物体的动能,然后再一微分就得到了动力学方程,这是多么简洁统一的方法啊。可是拉格朗日法的缺点是它的效率太低了。对于4自由度以下的机械臂,计算符号解的时间我们还能忍受。至于6自由度以上的机械臂,大多数人都没这个耐心了(十几分钟到数小时)。而且计算出来的动力学是一大坨复杂的公式,很难分析利用。所以本文我们采用牛顿-欧拉法建立机械臂的动力学模型(更准确的说是它的升级版——迭代牛顿-欧拉法)。
7.1 惯性参数
早期工业机器人不使用动力学模型是有原因的,一个是动力学的计算量太大,在高效的计算方法被发现之前,早年的老计算机吃不消;另一个原因就是动力学需要惯性参数。运动学只需要几何参数,这些相对好测量;可是动力学不仅需要几何参数,还需要惯性参数。测量每个连杆的质量、质心的位置、转动惯量很麻烦,尤其是当连杆具有不规则的形状时,精度很难保证。如果使用动力学带来的性能提升并不明显,谁也不想给自己找麻烦。
要使用动力学模型,惯性参数必不可少。例如 Robotics Toolbox 工具箱中[2]的 mdl_puma560.m 文件就存储了 PUMA-560 机器人的惯性参数。不同型号的机器人具有不同的惯性参数,而且机器人抓住负载运动时,也要把负载的惯性考虑进来。
有些情况下,我们不需要知道很精确的惯性参数,差不多够用就行了;可是有些场合对精度有要求,比如拖动示教就要求参数与实际值的误差一般不能超过10%。对于精度要求不高的场合,可以使用一个近似值。大多数三维建模软件(例如 SolidWorks、CATIA)以及一些仿真软件(例如 Adams)都提供惯性计算功能,一些数学软件(Mathematica)也有用于计算惯性的函数(我没有对比过,所以不敢保证这些软件的计算结果都是一样的,我估计很有可能是不一样的)。本文以 SolidWorks 为例介绍如何获取惯性参数。
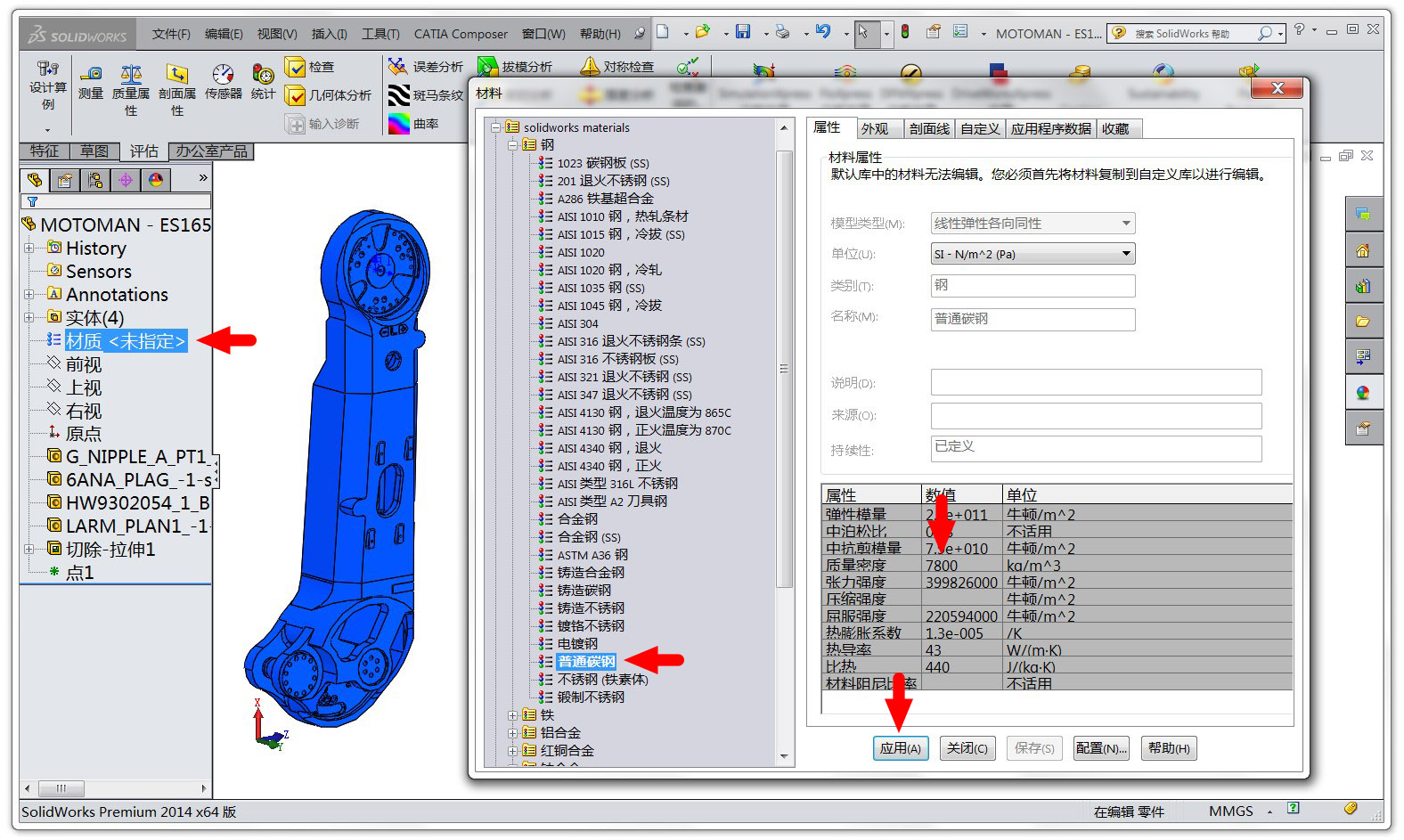
计算之前首先要设置连杆的材质。在 SolidWorks 中打开一个连杆,在左侧的“材质”上单击右键弹出“材料”对话框,如下图所示。在这里可以设置机器人本体的材质,MOTOMAN-ES165D 这款机器人的连杆是铸铝(铸造铝合金:Cast Aluminum)制造的。不过连杆不包含电机等部件,为此选择密度大一点的材料,本文选择钢铁。这里最重要的是材料的密度,钢铁的密度一般是7.8吨/立方米(在计算惯性时,软件假设连杆的密度是均匀的,这明显是简化处理了)。设置好后点击应用即可。
然后在上方“评估”选项卡中单击“质量属性”就会弹出如下图所示的对话框。
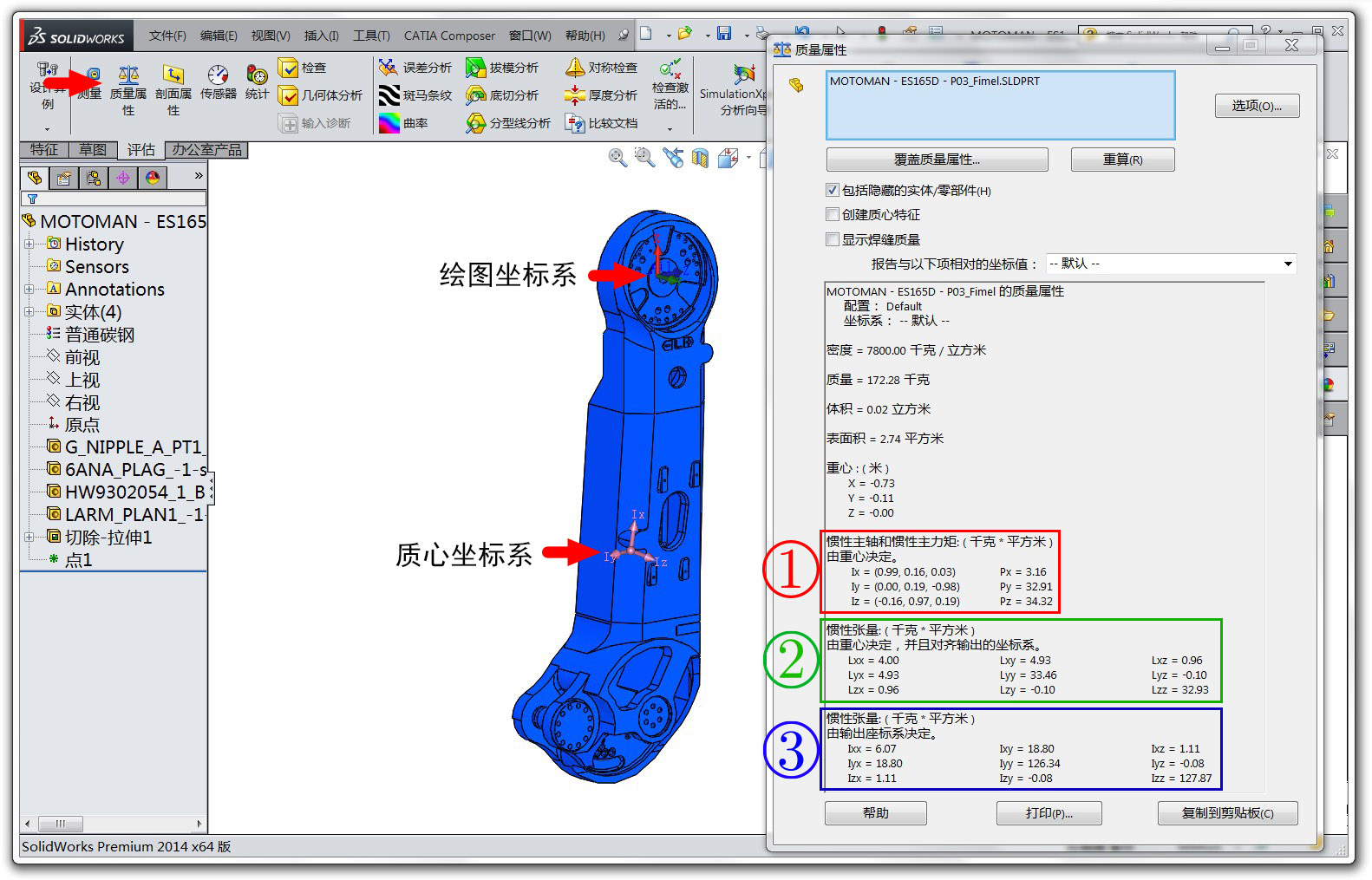
SolidWorks 很快就计算出了这个连杆的所有惯性参数。不过这里的信息量有点大,我逐个说明:
● 首先是连杆的质量:172.28 千克。如果你显示的单位不是千克,可以在当前对话框中的“选项”中修改单位。
● 然后是连杆的质心(或重心)坐标系,重心坐标系的原点也给出了:$(X,Y,Z)=(-0.73,-0.11,0)$,注意它是相对于绘图坐标系的哦。重心坐标系的姿态下面会解释。
● 最后是连杆的惯性张量,这个有些人可能不懂,我详细解释下。SolidWorks列出了3个惯性张量,它们之间的区别就在于分别相对于不同的坐标系:
① 相对于质心坐标系;其中的 Ix、Iy、Iz 三个向量表示质心坐标系相对于绘图坐标系的姿态(也就是质心坐标系的 x、y、z 三个轴向量在绘图坐标系中的表示),而 Px、Py、Pz 表示惯性主力矩(你要问我是怎么知道的,点“帮助”按钮)。惯性张量的形式是对角矩阵:
$$
\mathcal{I}_{\mathrm{A}}=\left[\begin{array}{ccc}
\mathrm{Px} & 0 & 0 \\
0 & \mathrm{Py} & 0 \\
0 & 0 & \mathrm{Pz}
\end{array}\right]
$$
② 相对于原点与质心坐标系重合,但是各轴与绘图坐标系一致的坐标系。SolidWorks只给出了惯性张量中各项的值。惯性张量的完整形式是对称矩阵(注意里面的负号):
$$
\mathcal{I}_{B}=\left[\begin{array}{ccc}
L x x & -L x y & -L x z \\
-L y x & L y y & -L y z \\
-L z x & -L z y & L z z
\end{array}\right]
$$
③ 相对于绘图坐标系(SolidWorks中称为输出坐标系),惯性张量的形式也是对称矩阵(同样注意里面的负号):
$$
\mathcal{I}_{C}=\left[\begin{array}{ccc}
I x x & -I x y & -I x z \\
-I y x & I y y & -I y z \\
-I z x & -I z y & I z z
\end{array}\right]
$$
这三个惯性张量都反映了同一个连杆的性质,因此应该是等价的。那么它们之间有什么关系吗?有的,它们之间可以转换。如果定义旋转矩阵 $R=(\rm Ix,Iy,Iz)$ ,质心坐标向量 $p=(X,Y,Z)$ ,连杆质量为 $m$,那么有
$$
\mathcal{I}_{B}=R^{\mathrm{T}}\mathcal{I}_{A}R\\
\mathcal{I}_{C}=\mathcal{I}_{B}+m S^{\mathrm{T}}(p) S(p)
$$
其中,$S(p)$ 表示向量 $p$ 的斜对称矩阵,这需要自定义函数(skew)实现,代码如下:
skew[v_] := {{0,-v[[3]],v[[2]]},{v[[3]],0,-v[[1]]},{-v[[2]],v[[1]],0}} 这组公式来自于[6],我已经验证过了,是正确的(要想结果比较接近,这些惯性参数至少要取到小数点后 5 位,这依然是在“选项”页中设置)。
我们得到了三个惯性张量,在动力学方程中我们应该使用哪个呢?下面的程序使用了$\mathcal{I}_{C}$,因为它是相对于绘图坐标系的,而我建立运动学时选择的局部坐标系就是绘图坐标系。
7.2 单刚体转动动力学
机械臂是一个多刚体,多刚体的动力学相互耦合是非常复杂的。所以,在研究多刚体动力学之前,我们先研究一个简单的情况,也就是单个刚体的动力学。对于一个刚体来说,它的直线运动我们不是很感兴趣,因为用初中物理的牛顿第二定律就能解决,所以我们只看转动的部分,毕竟转动有点难度,也有点意思。
假如我带着块砖头上了空间站。在失重状态下,如果我用手拨动一下砖头,随便给它一个初始的角速度,那砖头的运动是什么样的呢?就是下图所示的样子。这个例子的仿真代码也在我分享的链接里。
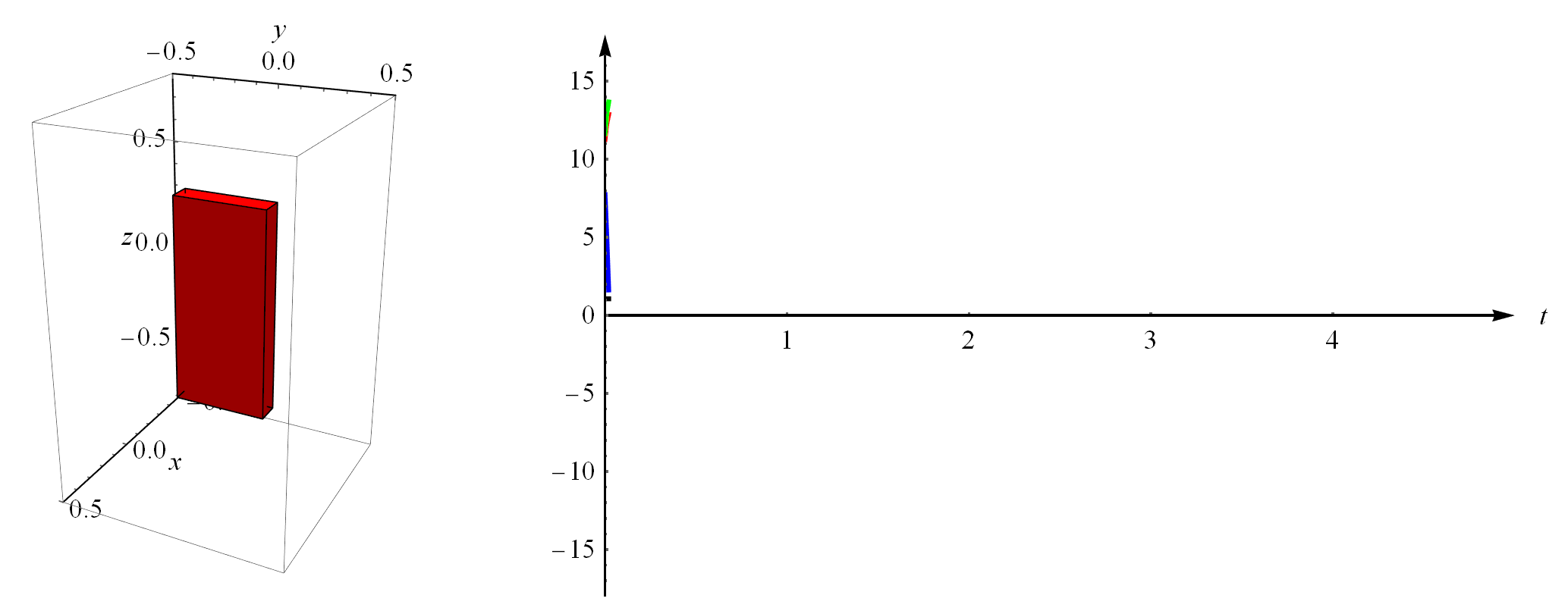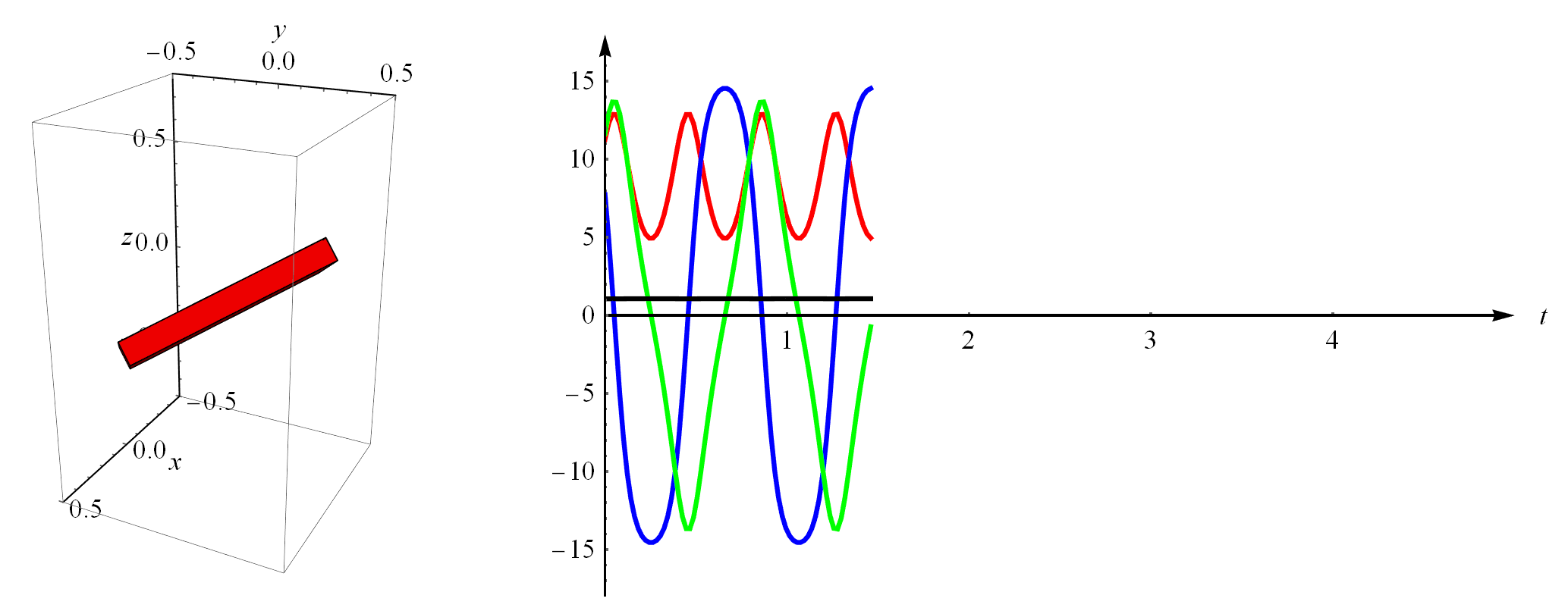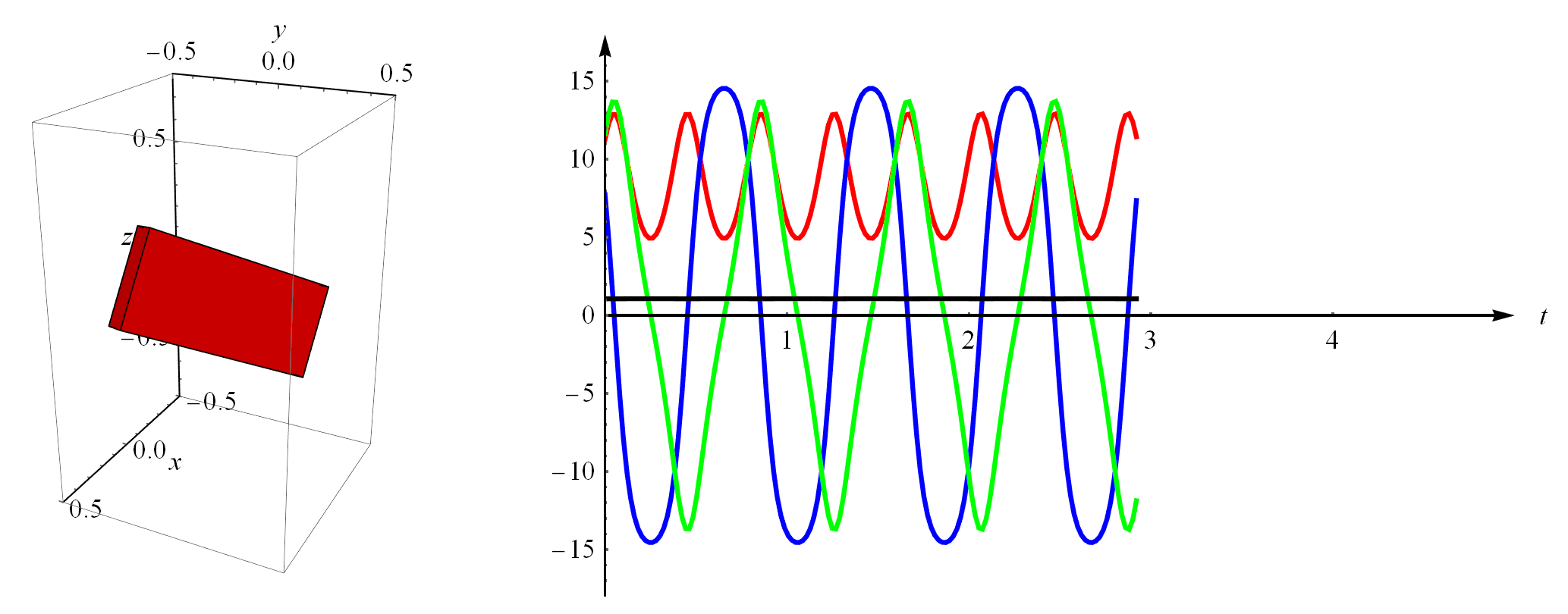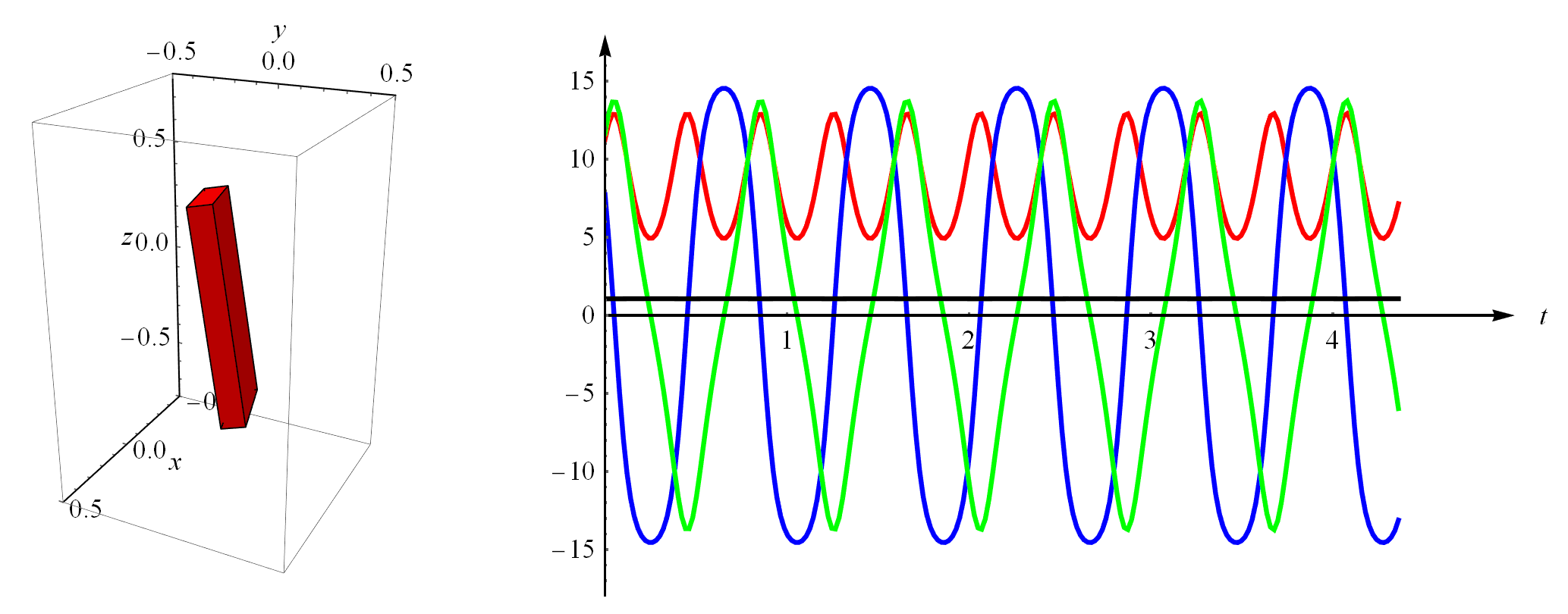
我们用的动力学方程就是描述转动的欧拉方程,如下。其中,$\mathcal{I}$就是砖头的转动惯量,它是个$3\times3$矩阵,而且是表示在自身坐标系下的(自身局部坐标系就是位于砖头质心且方向垂直于各平面的坐标系,这里就不画出来了)。$\omega$是砖头的角速度,注意它是个向量,即$\omega=({\omega}_x,{\omega}_y,{\omega}_z)^T$,同样它也是表示在自身局部坐标系下的。$\tau$表示力矩,它也是个三维向量,当然在这个例子里我只是给砖头一个初始速度,砖头转动过程中我不再干扰它,也假设没有任何阻力,所以始终有$\tau=0$。$\times$表示两个向量的叉乘。
$$\mathcal{I}\dot{\omega}+\omega\times\mathcal{I}\omega=\tau$$
砖头的姿态如何表示呢?为了简单一些,我直接用$3\times3$的旋转矩阵$R$来表示。旋转矩阵$R$与表示在自身坐标系中的角速度$\omega$的关系是什么呢?我们参照这篇论文《Explicit Newmark/Verlet algorithm for time integration of the rotational dynamics of rigid bodies》2.4节给出的计算方式,用角速度和角加速度去更新$R$。
在上面右图中,红绿蓝三色曲线分别是刚体的三个角速度,即$\omega=({\omega}_x,{\omega}_y,{\omega}_z)^T$,注意它们周期性地变化。图中还有一条黑色直线,那是砖头的角动量,因为砖头没有外部力矩作用,所以角动量守恒(守恒的意思就是不变,所以你看到一条平平的直线)。通过角动量守恒这一点我们也能看出来,仿真计算还是比较精确的。这篇文章采用的是类似于隐式欧拉的积分方法,比显式的欧拉积分要更精确。
转动是个相当有深度的话题,但是我们没太多时间在这里逗留,所以就举个例子吧。这个砖头还隐藏着一个有意思的现象,下面我给大家展示一下。同样的,我给它一个初始角速度,不过这次不是随便给的,这个角速度只给中间那个轴(按照三个轴的转动惯量从小到大排列,也就是y轴),然后给其它任意一个轴一点点扰动力矩($0.0001Nm$)以模拟空气等不理想情况下的扰动,再仿真一下,结果如下图所示。这就是有趣的网球拍效应(在抖音有很多介绍),这个效应说的是物体绕中间轴的转动总是不稳定的,本来好好地转动着却突然翻了个身。这个效应是在空间站上才被人类第一次发现的。这个现象刚被发现时还有点吓人,因为还有一个东西也在失重的环境里转动着,那就是我们的地球。反过来,如果你给最大的轴或者最小的轴一个初始速度,它们总是稳定的,不信你可以仿真试试。关于网球拍效应的解释,可以看这里:运动员的旋空翻与欧拉-潘索运动 。
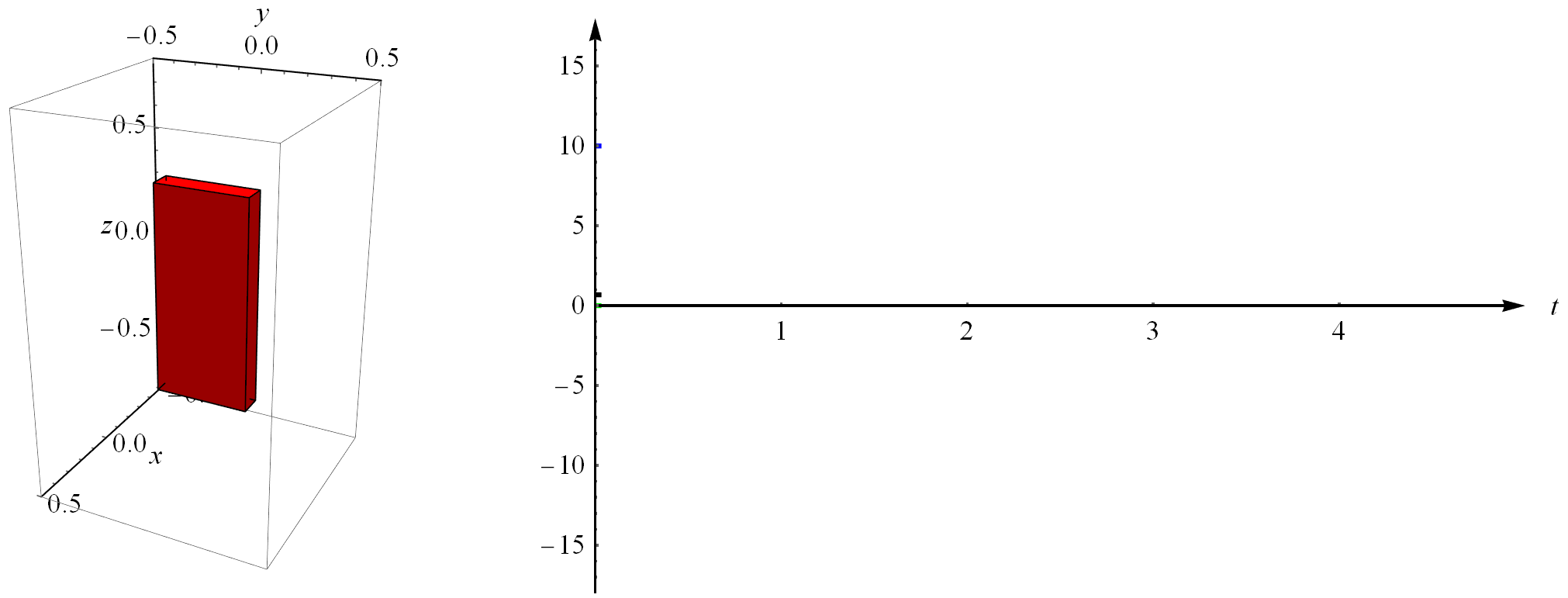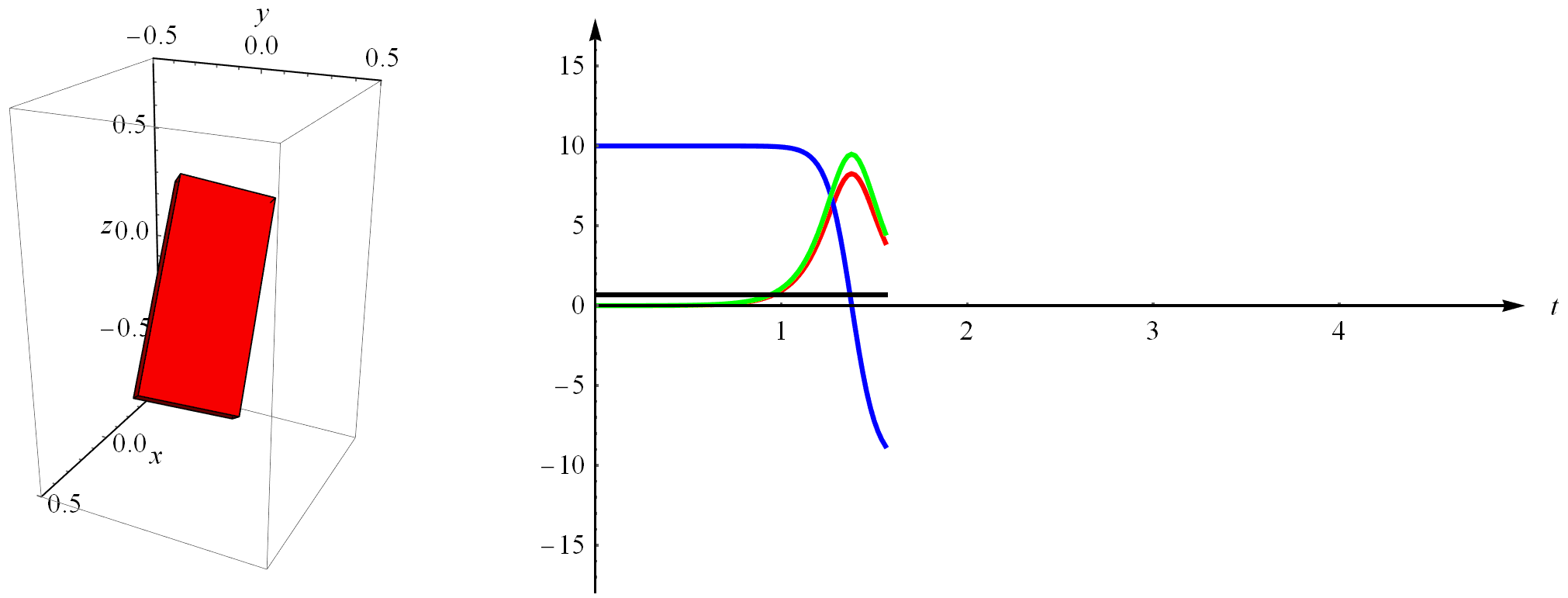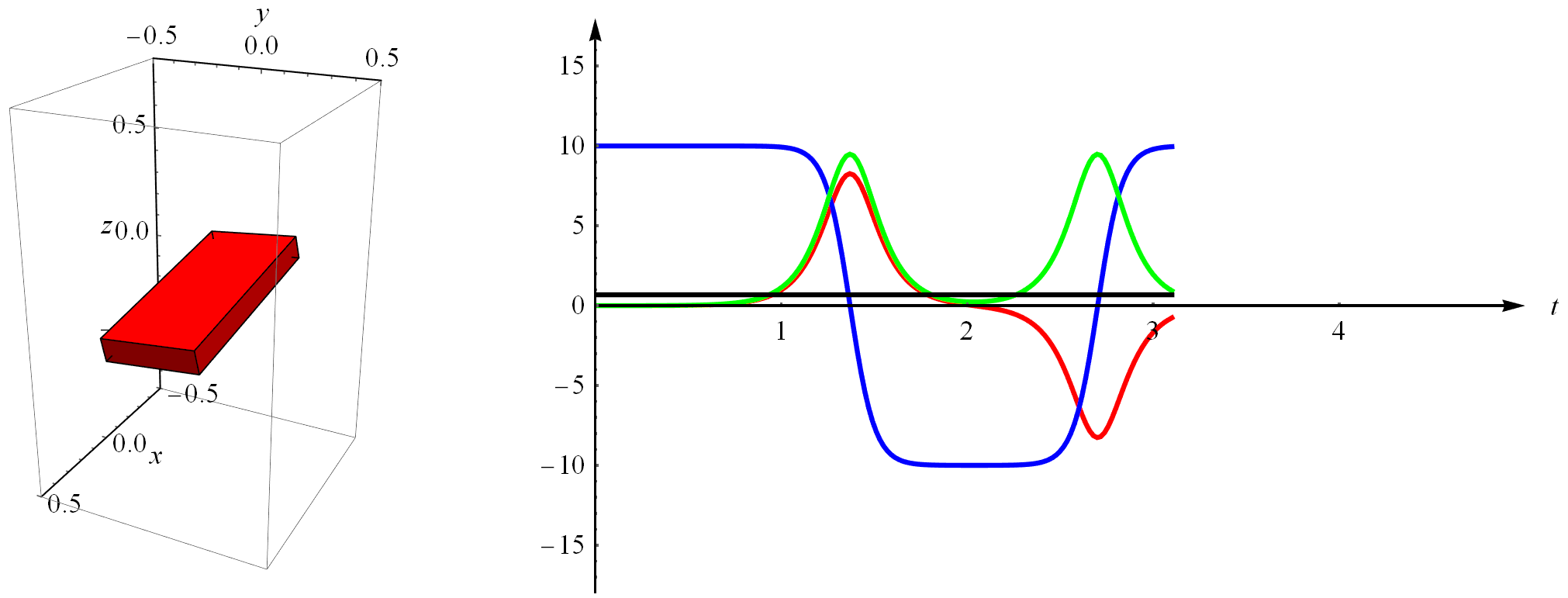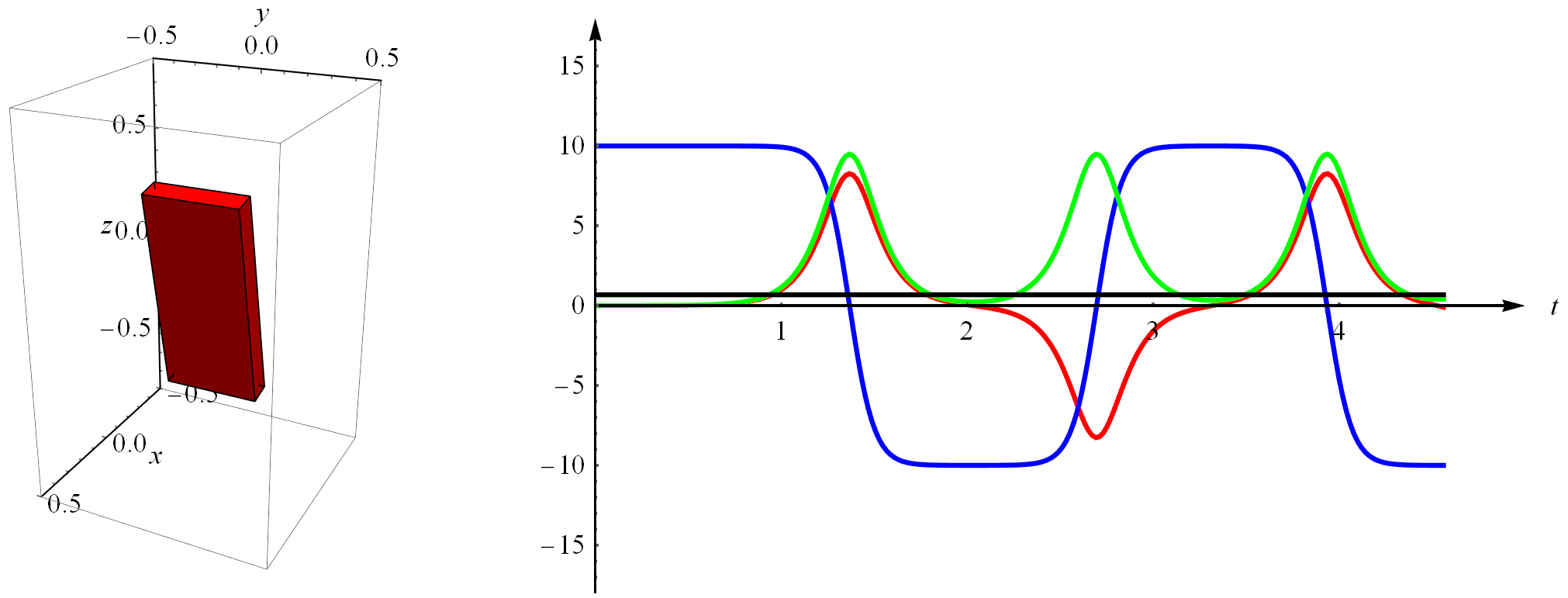

7.3 正动力学仿真
如果给你一条轨迹,如何设计控制律让机械臂(末端)跟踪这条轨迹呢,控制律的跟踪效果怎么样呢?借助正动力学,我们就可以检验所设计的控制律。
由于后面的程序所依赖的动力学推导过程[7]采用了相对自身的表示方法(也就是说每个连杆的速度、惯性、受力这些量都是相对于这个连杆自身局部坐标系描述的),旋量也是如此,为此需要重新定义旋量(代码如下)。其实旋量轴的方向没变(因为局部坐标系的姿态与全局坐标系一样),只是改变了轴上点的相对位置。
\[Xi]rb = Table[\[Omega]a[i] = axesDirInGlobal[[i]]; la[i] = axesPtInGlobal[[i]] - drawInGlobal[[i + 1]];
Join[Cross[-\[Omega]a[i], la[i]], \[Omega]a[i]], {i, n}];正动力学的 迭代牛顿-欧拉算法 代码如下,输入是力矩,输出是运动。可以看到,动力学模型比运动学模型复杂多了(动力学用到运动学,运动学却不需要动力学)。对于很多第一次接触机器人的同学来说,动力学是一只可怕的拦路虎,要搞明白十几个变量都是什么含义可不容易(在仿真的时候可能包含几十个变量,任何一个弄错了都会全盘皆输,动力学可比运动学难伺候多了)。因为动力学模型是一个微分方程,所以整个仿真过程就是个数值积分的过程。
endTime=10.0; steps=2000; dt=endTime/steps; (*参数初始化:仿真时长、步数、步长*)
gravityAcc=9.807; (*重力加速度大小*)
Do[mass[i]=1.0; gravity[i]=gravityAcc*mass[i]*{0,0,-1,0,0,0},{i,n+1}]; (*mass[i]表示第i个连杆的质量,具体值自己设,重力加速度沿z轴的负方向,即{0,0,-1,0,0,0}*)
Do[\[ScriptCapitalM][i]=IdentityMatrix[6],{i,n+1}]; (*\[ScriptCapitalM][i]表示第i个连杆的广义惯性矩阵,它包含质量和惯性张量*)
g[L[n+1],L[n+2]]=g[I,L[1]]=IdentityMatrix[4];
q=dq=ddq=ConstantArray[0,n]; (*关节角度、速度、加速度初始时刻假设都为0*)
Table[V[i]=dV[i]=ConstantArray[0,6],{i,n+1}]; (*连杆i的广义速度V[i]包括线速度和角速度,也假设开始时刻都为0*)
\[CapitalPi][n+2]=ConstantArray[0,{6,6}]; (*中间变量,没啥具体物理意义,只是迭代初始值*)
\[Beta][n+2]=ConstantArray[0,6]; (*也是中间变量*) (*以下是计算过程*)
qList=Table[
dq=dq+ddq*dt; q=q+dq*dt;(*欧拉积分*)
For[i=2,i<=n+1,i++, (*速度前向迭代,从第二个连杆开始到最后一个连杆*)
k=i-1; (*因为本文的连杆从1开始标记,所以第i个连杆依赖前一个(i-1)关节*)
g[L[i-1],L[i]]=TwistExp[\[Xi]r[[k]],q[[k]]].g[L[i-1],L[i],0];
g[I,L[i]]=g[I,L[i-1]].g[L[i-1],L[i]];
V[i]=Ad[Iv[g[L[i-1],L[i]]]].V[i-1]+\[Xi]rb[[k]]*dq[[k]];
\[Eta][i]=ad[V[i]-\[Xi]rb[[k]]*dq[[k]]].\[Xi]rb[[k]]*dq[[k]];
];
For[i=n+1,i>=2,i--, (*力和惯量后向迭代,从最后一个连杆开始到第二个连杆*)
k=i-1;
\[Tau][k] = 0.0; (*施加关节力矩*)
\!\(\*OverscriptBox[\(\[ScriptCapitalM]\), \(^\)]\)[i]=\[ScriptCapitalM][i]+T[Ad[Iv[g[L[i],L[i+1]]]]].\[CapitalPi][i+1].Ad[Iv[g[L[i],L[i+1]]]];
Fex[i]=T[Ad[RToH[HToR[g[I,L[i]]]]]].gravity[i];
\[ScriptCapitalB][i]=-T[ad[V[i]]].\[ScriptCapitalM][i].V[i]-Fex[i]+T[Ad[Iv[g[L[i],L[i+1]]]]].\[Beta][i+1];
\[CapitalPsi][i]=1/(\[Xi]rb[[k]].\!\(\*OverscriptBox[\(\[ScriptCapitalM]\), \(^\)]\)[i].\[Xi]rb[[k]]);
\[CapitalPi][i]=\!\(\*OverscriptBox[\(\[ScriptCapitalM]\), \(^\)]\)[i]-\[CapitalPsi][i]*KroneckerProduct[\!\(\*OverscriptBox[\(\[ScriptCapitalM]\), \(^\)]\)[i].\[Xi]rb[[k]],\[Xi]rb[[k]].\!\(\*OverscriptBox[\(\[ScriptCapitalM]\), \(^\)]\)[i]];
\[Beta][i]=\[ScriptCapitalB][i]+\!\(\*OverscriptBox[\(\[ScriptCapitalM]\), \(^\)]\)[i].(\[Eta][i]+\[Xi]rb[[k]]*\[CapitalPsi][i]*(\[Tau][k]-\[Xi]rb[[k]].(\!\(\*OverscriptBox[\(\[ScriptCapitalM]\), \(^\)]\)[i].\[Eta][i]+\[ScriptCapitalB][i])));
];
For[i=2,i<=n+1,i++, (*加速度前向迭代,从第二个连杆开始到最后一个连杆*)
k=i-1;
ddq[[k]]=\[CapitalPsi][i]*(\[Tau][k]-\[Xi]rb[[k]].\!\(\*OverscriptBox[\(\[ScriptCapitalM]\), \(^\)]\)[i].(Ad[Iv[g[L[i-1],L[i]]]].dV[i-1]+\[Eta][i])-\[Xi]rb[[k]].\[ScriptCapitalB][i]);
dV[i]=Ad[Iv[g[L[i-1],L[i]]]].dV[i-1]+\[Xi]rb[[k]]*ddq[[k]]+\[Eta][i]
];
q , {t, 0, endTime, dt}];//AbsoluteTiming (*显示计算耗时*) 其中, ad 函数用于构造一个李代数的伴随表达形式,代码如下。(开始我们定义的关节旋量是李代数,这里连杆的本体速度也是一个李代数,但加速度却不是。实际上,要想把加速度搞明白可不是那么容易的事[8])
ad[\[Xi]_] := Module[{w, v},
v = skew[\[Xi][[1 ;; 3]]]; w = skew[\[Xi][[4 ;; 6]]];
Join[Join[w, v, 2], Join[ConstantArray[0, {3, 3}], w, 2]] ] 正动力学的输入是关节力矩,下面我们为关节力矩设置不同的值,看看机械臂的表现:
● 如果令关节力矩等于零(即 \[Tau][k] = 0.0),机械臂将在唯一的外力——重力作用下运动,如下图所示。
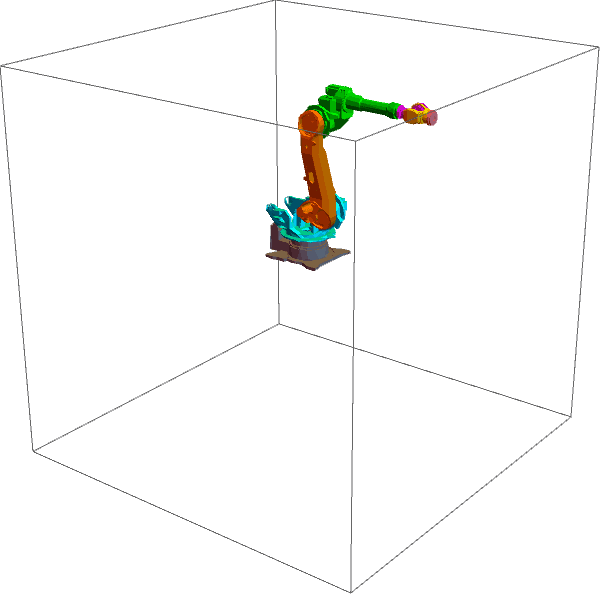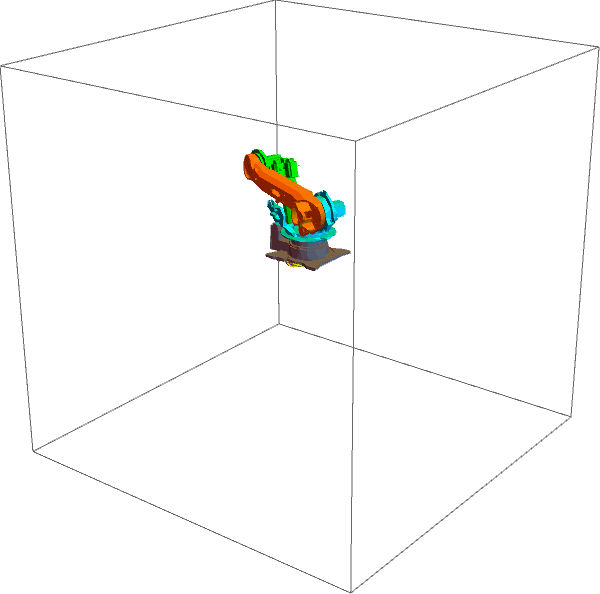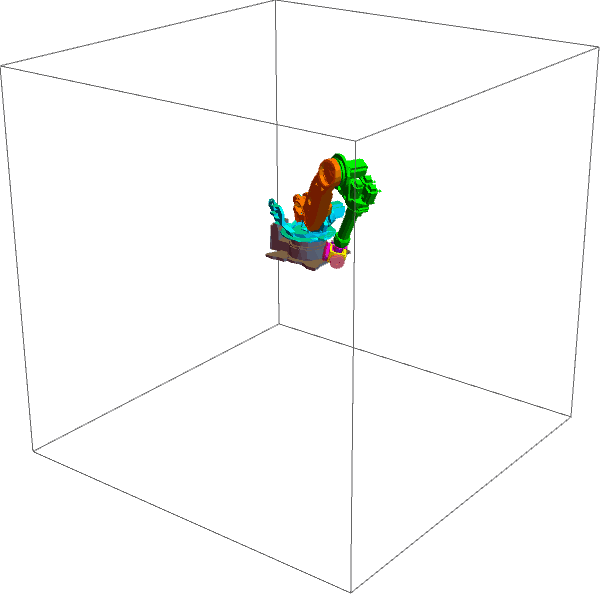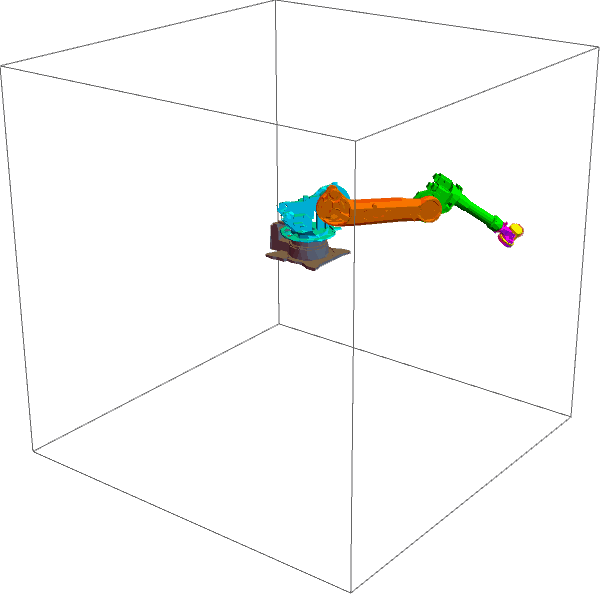
只受重力的情况下,机械臂的总能量应该守恒。我们可以动手计算一下机械臂的能量(由动能和重力势能组成,代码如下)。将仿真过程中每一时刻的能量计算出来并保存在一个列表中,再画出图像,如下图所示。可见能量几乎不变(轻微的变化是由积分误差导致的,如果步长取的再小一些,就更接近一条直线),这说明机械臂的总能量确实保持恒定,这也间接证实了正动力学代码的正确性。这个简单的事实让人很吃惊——虽然机械臂的运动看起来那么复杂,但是它的能量一直是不变的。从力和运动的角度看,机械臂的行为变化莫测,可是一旦切换到能量的角度,它居然那么简洁。机械臂的运动方程和能量有什么关系呢?聪明的拉格朗日就是从能量的角度去推导动力学方程的。
totalEnergy = Total@Table[1/2*V[i].\[ScriptCapitalM][i].V[i] + mass[i]*gravityAcc*g[I, L[i]][[3, 4]], {i, n + 1}];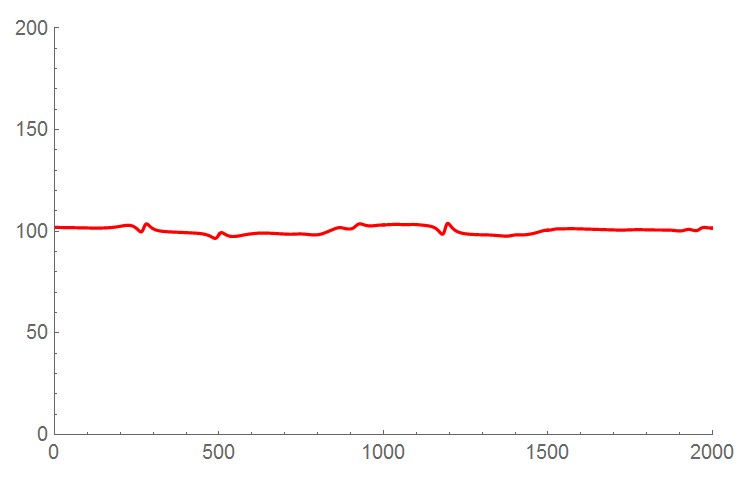
● 我们也可以让机械臂跟踪一条给定的轨迹,此时给定力矩为 PD 控制律:
Kp=10000; Kd=50; (*PD 控制系数,需要自己试探选取*)
\[Tau][k]=Kp(qfun[k][t]-q[[k]])+Kd(dqfun[k][t]-dq[[k]]); 其中,qfun 和 dqfun 是 4.2 节中定义的插值函数,这里用作机械臂要跟踪的(关节空间中的)参考轨迹。跟踪一个圆的效果如下图所示。

● 机械臂在实际工作时可能会受到干扰。PD控制律对于扰动的效果怎么样?我们施加一个扰动信号试试。这里我选择一个尖峰扰动,模拟的实际情况是机械臂突然遭受了一个撞击。扰动函数的定义代码如下,你可以自己修改扰动的大小和尖峰出现的时间。
Manipulate[disturb[t_] := peak Exp[-fat(t - tp)^2];
Plot[disturb[t], {t, 0, 10}, PlotRange -> All], {peak, 50, 300, 0.1}, {fat, 0.5, 40, 0.1}, {tp, 0, 10, 0.1}, TrackedSymbols :> True]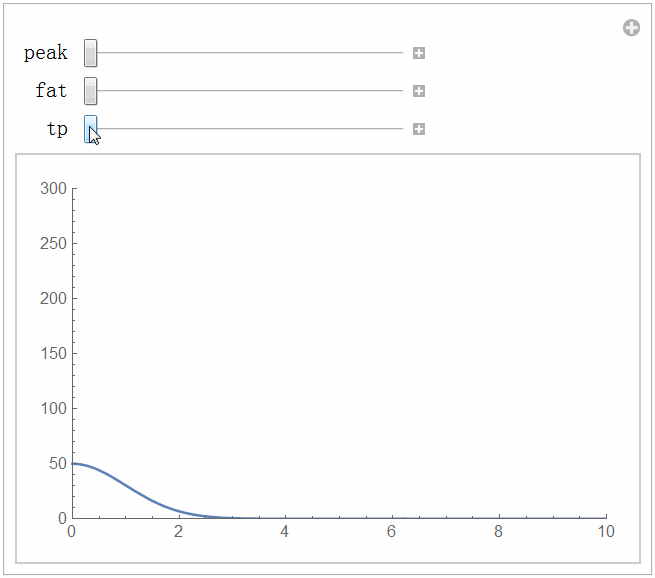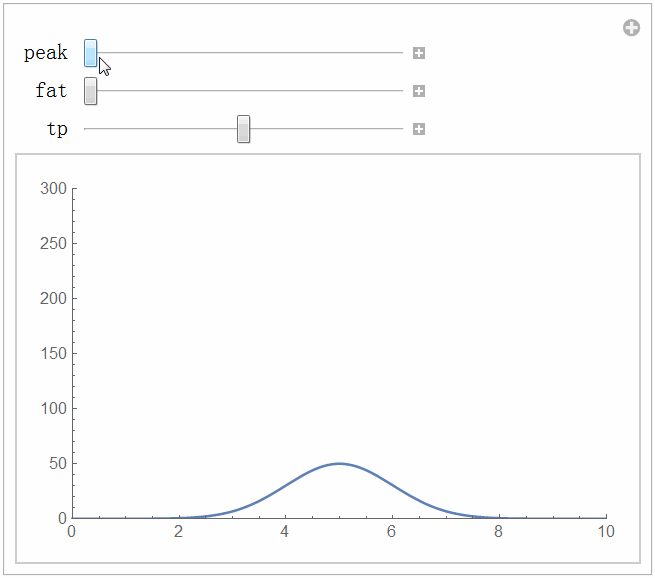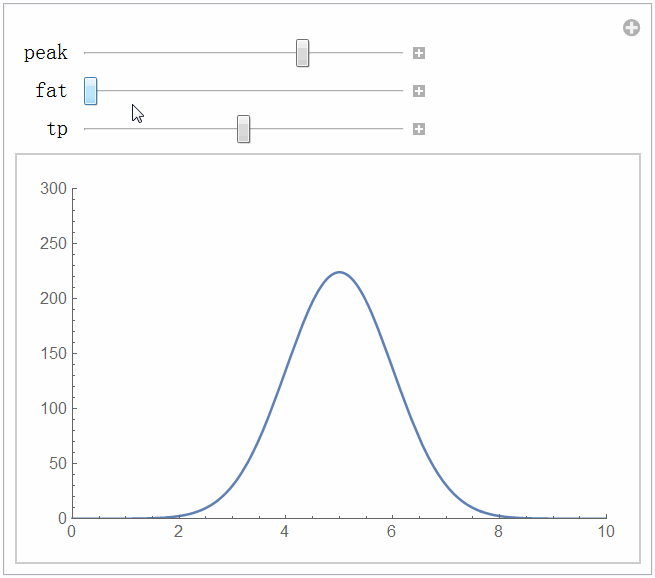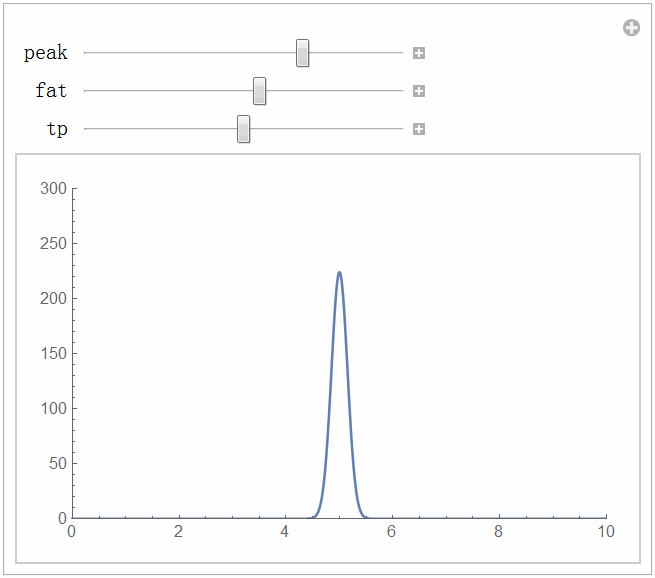

把扰动加到第二个关节的力矩上
\[Tau][k] = Kp (0 - q[[k]]) + Kd (0 - dq[[k]]) + If[k == 2, disturb[t], 0];机械臂的响应如上右图所示,可见机械臂还是能回复零点姿势的。一开始机械臂有一个轻微的颤动,俗称“点头”。这是由于刚一开始机械臂的角度和角速度都为零,所以关节力矩也为零,导致机械臂缺少能够平衡重力的驱动力。在第5秒左右扰动出现,导致机械臂偏离了零点姿势,但在反馈控制作用下很快又回到了零点姿势。
7.4 逆动力学仿真
输入力矩后,借助正动力学能得到关节角加速度,积分后可以得到角速度和角度。就像运动学和逆运动学的关系一样,逆动力学与正动力学刚好相反,它的用处是:如果告诉你机械臂的运动(也就是关节角度、角速度、角加速度),计算所需的关节力矩。
{endTime,steps}={10.0,1000};
dt=endTime/steps; (*还是参数初始化*)
gravityAcc=9.807; (*重力加速度*)
Do[mass[i]=1.0; gravity[i]=gravityAcc*mass[i]*{0,0,-1,0,0,0},{i,n+1}];
Do[\[ScriptCapitalM][i]=IdentityMatrix[6]; V[i]=dV[i]=ConstantArray[0,6],{i,n+1}];
Fin[n+2]=ConstantArray[0,6]; (*第n+1个连杆受到的内力,为了迭代过程写起来方便定义的*)
g[L[n+1],L[n+2]]=g[I,L[1]]=IdentityMatrix[4];
q=dq=ddq=ConstantArray[0,n]; (*初始状态的关节角度、速度、加速度*)
\[Tau]List=Table[
For[i=2,i<=n+1,i++, (*速度前向迭代:从第二个连杆开始到最后一个连杆*)
k=i-1;
g[L[i-1],L[i]]=TwistExp[\[Xi]r[[k]],q[[k]]].g[L[i-1],L[i],0];
g[I,L[i]]=g[I,L[i-1]].g[L[i-1],L[i]];
V[i]=Ad[Iv[g[L[i-1],L[i]]]].V[i-1]+\[Xi]rb[[k]]*dq[[k]];
dV[i]=Ad[Iv[g[L[i-1],L[i]]]].dV[i-1]+ad[V[i]-\[Xi]rb[[k]]*dq[[k]]].\[Xi]rb[[k]]*dq[[k]]+\[Xi]rb[[k]]*ddq[[k]]];
For[i=n+1,i>=2,i--, (*力后向迭代:从最后一个连杆开始到第二个连杆*)
k=i-1;
Fex[i]=T[Ad[RToH[HToR[g[I,L[i]]]]]].gravity[i]; (*连杆受到的重力*)
Fin[i]=\[ScriptCapitalM][i].dV[i]-T[ad[V[i]]].\[ScriptCapitalM][i].V[i]+T[Ad[Iv[g[L[i],L[i+1]]]]].Fin[i+1]-Fex[i];
\[Tau][k]=\[Xi]rb[[k]].Fin[i]];
Array[\[Tau],n]
, {t, 0, endTime, dt}];//AbsoluteTiming在重力作用下,机械臂保持“立正姿势”需要多大力矩呢?将初始状态设为0,经过逆动力学计算得到的答案是 {0,-38.1,-38.1,0,-2.06,0}。如果把这个力矩再带入正动力学仿真就能看到机械臂保持静止不动,这证明我们的逆动力学模型也是正确的。
8. 结尾
本文以 Mathematica 通用数学计算软件为平台,针对串联机械臂的建模、规划和控制中的基础问题进行了仿真。
9. 补充: Mathematica 的缺点
在笔者就读研究生期间,Matlab 的使用率颇高。每次参加答辩、听报告,看着同学或老师用 Matlab 制作的丑陋不堪的图表和动画,心中就想把 Matlab 的界面设计师枪毙十分钟。再加上呆板的函数定义和使用方式、缺乏对部分机器人仿真功能的支持,让我不得不寻找其它的替代软件。可是在网络发达的今天,我居然找不到稍微像点样的介绍机器人仿真的文章以及原理性代码,要么过于低端,要么是东拼西凑,于是想把自己的经验写出来,并公开代码。
就像 Matlab 有很多让人不爽的地方一样,Mathematica 用于机器人仿真同样存在一些缺陷。我们之前在碰撞检测部分已经提过,要想达到很快的检测速度就不得不使用简单的几何模型。虽然 Mathematica 的函数也经过了优化,但是只适用于需要较少计算次数的场合,在多次处理大量数据时还是比较慢。Mathematica 本身是用 C 语言写成的,如果某个函数被大量调用可以考虑用 C 语言写成动态链接库(dll),然后在 Mathematica 中调用,这就像 Matlab 中的 MEX 文件。
调试找错是个痛苦的过程,在 Mathematica 中更是这样。Mathematica 支持调试时设置中断,可惜使用起来不太方便。Mathematica 提供了一个专门用来开发调试的软件——Workbench,操作同样繁琐。 在调试时,我只好使用 Print 函数打出中间计算结果来检查程序是否正确。Mathematica 缺少像 Matlab 一样的变量监控窗口可以实时看到变量的值,这在调试时显得很不方便(虽然在堆栈中可以监视局部变量)。所以,尽量不要在 Mathematica 中使用中断[9]。Matlab 中如果出现语法错误,编译会中止并显示出错位置,但在 Mathematica 中却不会自动停止,它仿佛像推土机一样停不下来。一旦出错你通常只会在计算结果中看到一堆冗长的代码,却很难发现错在哪了。对于包含许多步的计算过程,调试起来可能很浪费时间,最好的方法是把代码切割成功能简单清晰的模块,挨个检验每个模块要比检验一堆纠缠不清的代码更容易。
参考文献
[1] 一种高效的开放式关节型机器人3D仿真环境构建方法,甘亚辉,机器人,2012.
[2] Robotics, Vision and Control Fundamental Algorithms in MATLAB, Peter Corke.
[3] A Mathematical Introduction to Robotic Manipulation —— A Mathematica Package for Screw Calculus, Richard M. Murray, 435页.
[4] Robotica: A Mathematica Package for Robot Analysis, Mark W. Spong, IEEE Robotics & Automation Magazine, 1994.
[5] 机器人学导论,John J. Craig,中文第三版.
[6] Robotics - Modelling, Planning and Control, Bruno Siciliano, 582页.
[7] Lie Group Formulation of Articulated Rigid Body Dynamics, Junggon Kim, 2012.
[8] The Acceleration Vector of a Rigid Body, Roy Featherstone, The International Journal of Robotics Research, 2001.
[9] Automatically Add Debug Contents to a Program, StackExchange, 2016.
Do you mind if I quote a few of your posts as long as I provide credit and sources back
to your weblog? My blog is in the exact same area of interest as yours and my users would really benefit from a lot of the information you provide here.
Please let me know if this okay with you. Thank you!
I’m ok with that. I’m glad to see my posts are helpful to others.